8/23/18
Many Body 621
Spring 2024
| Images | Texts |
Exercises |
Times of Course |
Syllabus outline |
Timetable |
 |
|
Magic Angle Graphene |
Illustrating the Effective Action in Path Integral |
Relationship between Meissner Effect and Phase Rigidity of a Superconductor. |
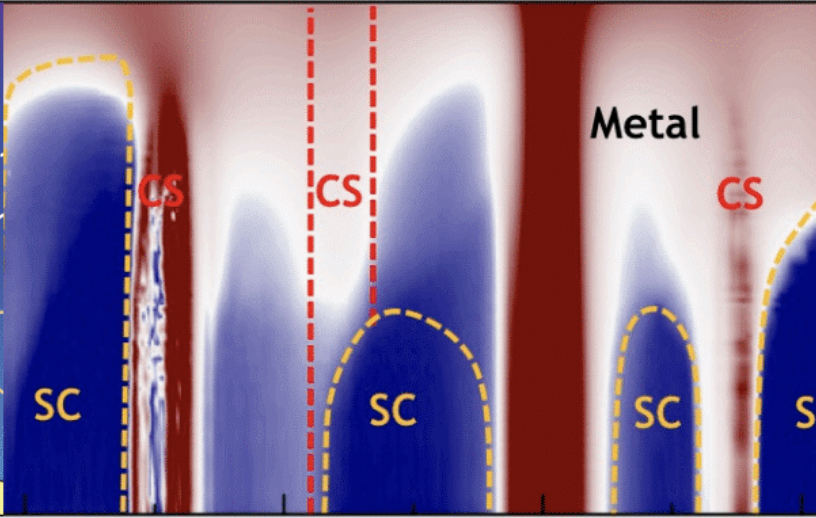
Gap Structure of a d-wave superconductor |
 |
|
Phase Diagram of the Kondo Effect |
CeCoIn5: a 115 Superconductor |
Instructor: Piers Coleman, Room 268
If you have any questions about this course or the
homework, please do not hesitate to contact me via email
at : coleman@physics.rutgers.edu
Scope of Course. This course continues from Many
Body 620, and will introduce many body physics needed to
understand current research activities in quantum
condensed matter, including finite temperature methods,
response functions, path integrals, conventional and
unconventional superconductivity, strongly correlated
electron systems. I will also review essential
material and offer additiional tuition to cater to those
who were unable to take 620 last semester. Please
ask Shirley Hinds for a special permission to register.
There will be a lot of discussion and interaction. Please
register as soon as possible.
-
Here are some additional useful references:
- Condensed Matter Field Theory by Alexander Altland and Ben Simons.(CUP, 2006)
- Advanced Solid State Physics by Philip Phillips, second edition (CUP, 2012).
- Basic Notions in Condensed Matter Physics by P. W. Anderson, Benjamin Cummings 1984. A classic reference. Many of us still turn to this book for inspiration, and philosophy. It also has a fine selection of important reprints at the back.
-
Quantum Field Theory in Condensed Matter Phyiscs, A. M. Tsvelik, Cambridge University Press, 2nd edition (2003).
- R. Shankar, Rev Mod Phys 66 129 (1994). An amazingly self-contained review of the renormalization group and functional integral techniques written by one of the best expositors of condensed matter physics.
- ``Field Theories of Condensed Matter Physics'' by E. Fradkin. (Frontiers in Physics, Addison Wesley). Interesting material on the fractional statistics and the fractional quantum Hall effect.
- ``Methods of Quantum Field Theory in Statistical Physics'' by Abrikosov, Gorkov and Dzyalozinskii. (Dover Paperback) - Classic text from the sixties, known usually as AGD.
- ``A guide to Feynman Diagrams in the
Many-Body problem by R. D. Mattuck. A light
introduction to the subject. Reprinted by Dover.
- ``Greens functions for Solid State Physics'' S.Doniach and E. H. Sondheimer. Not as thorough as AGD, but less threatening and somehow more manageable. Frontiers in Physics series no 44.
- ``Quantum Many Particle Systems'' by J. W. Negele and H. Orland. Alas all the good physics is in the unsolved exercises! However, it is the only one of this set to touch on the subject of functional integrals.
- The Theory of Quantum Liquids by D. Pines and P. Nozieres. Excellent introduction to Fermi liquid theory that avoids the use of field theory.
- Statistical Physics, vol II by Lifshitz and Pitaevskii. Pergammon. Marvellous book on applications of many body physics, mainly to condensed matter physics.
Traditional Many Body Theory and Greens Functions
Further references:
Some
Online references (Check it out- this is a great
link).
Exercises 621 (Return to top)
Exercise
1 Solution
to Exercise 1
Exercise
2 Solution to Exercise 2
(Return to top)
Times: 12.10 Weds and 2 pm Friday in Serin 287. NOTE: We will start on Fri, Jan 19th. Occasionally, to make up for my travel, we will hold an additional class at a time to be decided.
Office hour: Time to be decided. Tel x 9033.
Assessment: I anticipate four take home exercises. I want to encourage an interactive class and will take this into account when grading.
(Return to top)
Outline Still to be finalized. This is a very
approximate outline that we will adjust after discussion
at the first class.
- Heavy Fermion Materials and the Kondo Lattice
- Anisotropic Superconductivity and High Tc.
- Twisted Bilayer Graphene
- Z2 gauge theories and Kitaev Spin Liquids
(Return to top)
Schedule: 2024 UNDER CONSTRUCTION Webpage from 2023
Week |
Extra class Possible Time: 3pm Mondays |
Weds 12.10-1.30 SRN 287 |
Friday 2.00-3.20pm SRN 287 |
| Jan 15-19 |
17 Jan No Class |
19 Jan L1 Introduction to Course Notes |
|
1 Jan 22-26 |
23 Jan L2 Local Moment Formation: the Anderson and Kondo Models. L2 Notes |
26
Jan L3 Green's functions, scattering, phase shifts and Friedel-Levinson theorem in the Anderson model. Heuristic derivation of the Kondo model. L3 Notes |
|
2 Jan 29-Feb 2 |
Jan 29 5pm Makeup Class L4 Renormalization Concept and the Schrieffer Wolff Transformation L4 Notes |
31st January L5 Poor Man Scaling in the Kondo Effect. L5 Notes |
2nd Feb L6 Large N Approximation L6_Notes |
3 Feb 5-9 |
Feb 5 5pm Makeup Class L7 Large N Solution to the Kondo impurity. L7 Notes |
7 Feb |
9 Feb Kondo insulators and Oshikawa's Theorem. L9_Notes |
4 Feb 12-16 |
14 Feb No Class |
16
Feb No Class |
|
5 Feb 19-23 |
21 Feb No Class |
23 Feb Retardation and Anisotropic Pairing The Anderson Morel Solution L10 Notes |
|
6 Feb 26-Mar 1 |
26 Feb Anisotropic Pairing I Mainly d-wave pairing L11 Notes |
28
Feb Anisotropic Pairing II L12 Notes |
1st
March Superfluid Helium 3 L13 Notes |
7. Mar 4 -8 |
6th
March No Class: March Meeting |
8th
March RVB Theory of Superconductivity and Kondo-Stabilized spin liquids L14 Notes |
|
8. Mar 11-15 |
Spring Break |
Spring Break |
|
9. Mar 18-22 |
22nd
March Class Cancelled |
24th
March Class Cancelled. |
|
10. Mar 25-29 |
29th
March Z2 Gauge Theories and Kitaev Spin Liquids L15 Notes |
31
March Kitaev Spin liquids in 2 and three dimensions. Jordan Wigner Approach L16 Notes |
|
11. Apr 1-5 |
April
3rd Kitaev Model continued L17 Notes |
April
5th The Toric Code L18 Notes |
|
12. Apr 8-12 |
April 8th The Toric Code L19 Notes |
April
10th The Z2 Gauged Ising Model L20 Notes |
No Class |
13. Apr 15-19 |
No Class |
April
17th The Yao Lee Model in three dimensions: A gapless spin liquid with a Fermi Surface. L21 Notes |
April 19th Beyond BCS: UTe2 and Kondo Kitaev (CPT) model. L22 Notes |
| 14.
Apr 22-26 |
April 22nd Twisted Bilayer Graphene: Bistritzer MacDonald Model I L23 Notes |
April
24th Twisted Bilayer Graphene Bistritzer MacDonald Model II L24 Notes |
April
26th Twisted Bilayer Graphene: The Heavy Fermion Picture L25 Notes |
15. Apr 29-May 3 |
April 29th Twisted Bilayer Graphene The Heavy Fermion Picture L26 Notes |
||
(Return to top)
