Introduction to Many Body Physics, Course 620, Fall 2009

Other courses

Computational physics

Many body 2004 by P. Coleman

B. Symons course



     
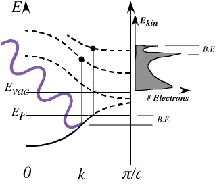
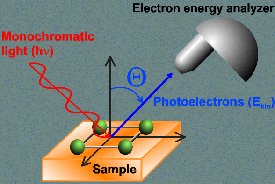
(a) Cuprate superconductor levitates a magnet, (b) Band structure and density of states of a material probed by ARPES (c) ARPES (Angle resolved photoemission spectroscopy) technique (d) Richard P. Feynman

Many body physics provides the framework for understanding the collective behavior of interacting electrons in a material. This course provides an introduction to the field, familiarize you with the main techniques and concepts, aiming to give you first-hand experience in calculations and problem solving using many body methods.

 

Class Time: ARC building (212), 12:00-1:20pm on Wednesday, 1:40-3:00pm on Friday

Instructor: Kristjan Haule
Office: Serin E267
email: haule@physics.rutgers.edu
Phone: 445-3881
Office hours: Friday 4:45pm



Texts: The course will be built from the two excellent books:

  1. Condensed Matter Field Theory by Alexander Atland and Ben Simons
    2. A modern textbook on Field Theory with strong emphasis on modern tools like Functional field integral.

  2. Many-Particle Physics by Gerald D. Mahan
    3. A classical textbook dealing in detail with response functions such as Green's function and optical conductivity and more general Kubo formalism.


Here are some other good references:
  1. Many Body Physics by Piers Coleman
    2. Great evolving monograph.
  2. Methods of Quantum Field Theory in Statistical Physics by A.A. Abrikosov, L.P. Gorkov, I.E. Dzyaloshinski
    3. Classic text from the sixties, known usually as AGD. Technically a bity more involved but contains many derivations which can not be found in any other book.
  3. Basic Notion of Condensed Matter Physics by P.W. Anderson
    4. Great inspiration from one of the "fathers" of strongly correlated field
  4. Quantum Thoery of Many-Particle Systems by A.L. Fetter and J.D. Walecka
  5. Field Theories of Condensed Matter Systems by Edwardo Fradkin
    6. Interesting material on the fractional statistics and the fractional quantum Hall effect.
  6. Introduction ot Superconductivity by Michael Tinkham
    7. Great book on supeconductivity.
  7. Interacting Electrons and Quantum Magnetism by Assa Auerbach
  8. Quantum Field Theory in Condensed Matter Physics by Alexei M. Tsvelik
    9. Very good for one dimensional systems. No excercises.



Course Outline and List of Topics

  1. Quantum fields
  2. Second quantization
  3. Applications of second quantization:
    4.
    1. Jellium model
    2. Tight binding model
    3. Mott Hubbard transition and Spin models of Mott insulator
    4. Interacting fermions in 1D
    5. Quantum spin chain
  4. Feynman path integral
  5. Functional field integral
    6.
  6. Green's function at zero temperature and finite temperature (Matsubara formalism)
  7. Perturbation Theory
  8. Plasma theory of interacting electron gass
  9. Bose-Einstein condensation and superfluidity
  10. Superconductivity & BCS Theory

Literature: Condensed Matter Field Theory by Alexander Atland and Ben Simons, Many-Particle Physics by Gerald D. Mahan (Only chapter 6 & 7)

Students with Disabilities