
Throughout your time in the course scientific notation will be extensively used. Therefore it is crucial that you develop an understanding of this particular style of representing typically small or very large numbers, where adding trailing or leading zeros becomes cumbersome. Here is a great Scientific Notation Reference that you should all look into.
For convenience I am including a table of commonly used prefixes in science (typically in increments of powers of 3), along with examples of physical units attached with these prefixes. If all of the units here do not make sense to you, this is perfectly fine. The actual physical unit could be considered a variable to which we attach a prefix.
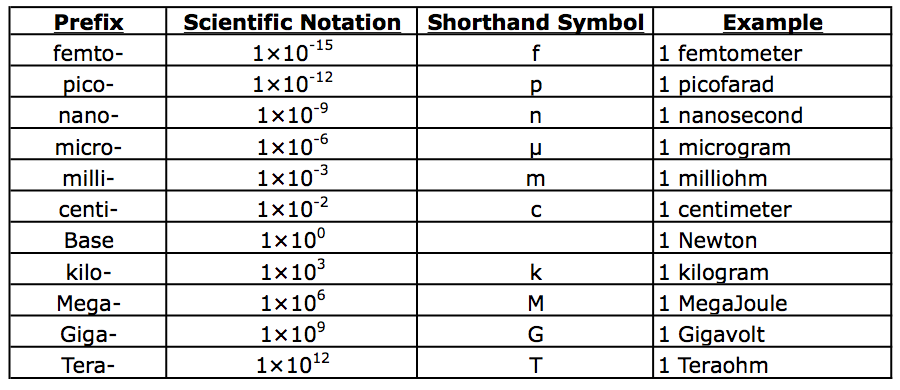
Besides gaining an understanding of scientific notation, you must become comfortable with the act of converting between different sets of units which represent that same type of general physical meaning such as mass, length, Temperature etc... I have included another link to a Dimensional Analysis Walkthrough that you should all go through. In general to convert units you are simply multiplying one physical value to another of the same type by multiplying by 1. This may seem a little misleading, but any definition for a unit conversion (ie. 12 inches = 1 foot) can be re-expressed as unity if we simply divide both sides of the equation by one term appearing on either side of the equation (ie. 12in⁄1ft=1). Of course when you do this though, you must arrange the fraction so it will cancel the units you do not want, and leave behind the units in which you wish the physical quantity expressed.
As an example of dimensional analysis I turn to a humorous utterance made by grandpa (Abraham Jay-Jedediah "Abe") Simpson on Matt Groening's, "The Simpsons" animated television program. In response to the metric system, Grandpa Simpson says, "The metric system is a tool of the devil! My car gets 40 rods to the hogshead and that's the way I likes it."
So our unit of measure that we are interested is a distance per unit volume of gas consumed. The unit we (in the USA and Great Britain anyway) all would know is miles per gallon, or m.p.g., so we will convert into these units from rods/hogshead.
1. We must find the relevant conversions between the units. Let us begin with length. One rod is the equivalent of 16.5 feet as defined in the English system of measure. We also know that there are 5,280 feet in one mile. We put this all together as follows,
$${1\:rod}\times\frac{16.5\:feet}{1\:rod}\times\frac{1\:mile}{5,280\:feet}=$$$$=3.125\times10^{-3}\:miles,\:\:\:\left(1\right)$$
which gives us our conversion between miles/rods yielding 320 rods in one mile (obtained by taking the reciprocal to the final answer in equation (1), and moving it to the other side).
2. Next we must find a conversion for going between the units of volume measured in hogsheads to the more familiar gallon. Looking this up, we find that there are 63 US gallons in 1 hogshead.
3. Now we put it all together as,
$$\frac{40\:rod}{1\:Hogshead}\times\frac{16.5\:feet}{1\:rod}\times\frac{1\:mile}{5,280\:feet}\times\frac{1\:Hogshead}{63\:gallons}=$$$$=\frac{40\:rod}{1\:Hogshead}\times\frac{1\:mile}{320\:rods}\times\frac{1\:Hogshead}{63\:gallons}=0.00198\:mpg.\:\:\:\left(2\right)$$
Note the atrocious mileage Grandpa Simpson used to get...
Unit conversions can be tricky, but dimensional analysis is a powerful tool in solving these problems.