
In astronomy we are limited by the fact that we are looking at the sky as a two-dimensional spherical shell in the sky with no immediate knowledge of the distance to an object, Hence the true size or width across the sky of an astrophysical object in physical units of distance like km or light-years is unknown. If we do have external information as to how wide an object is or how far away it is in physical units, we can use geometry to discover the unknown distance, physical size, or angular size of an astrophysical object.
The image below depicts the observer at the origin (0,0) of the figure below with a radius , r, that corresponds to the distance to some astrophysical object, and the angle θ is the angular size of said object. Let us now solve for the mathematical relationship, along with unit conversions, that show explicitly how an angular size translates to a physical size for some distance r away from the observer.
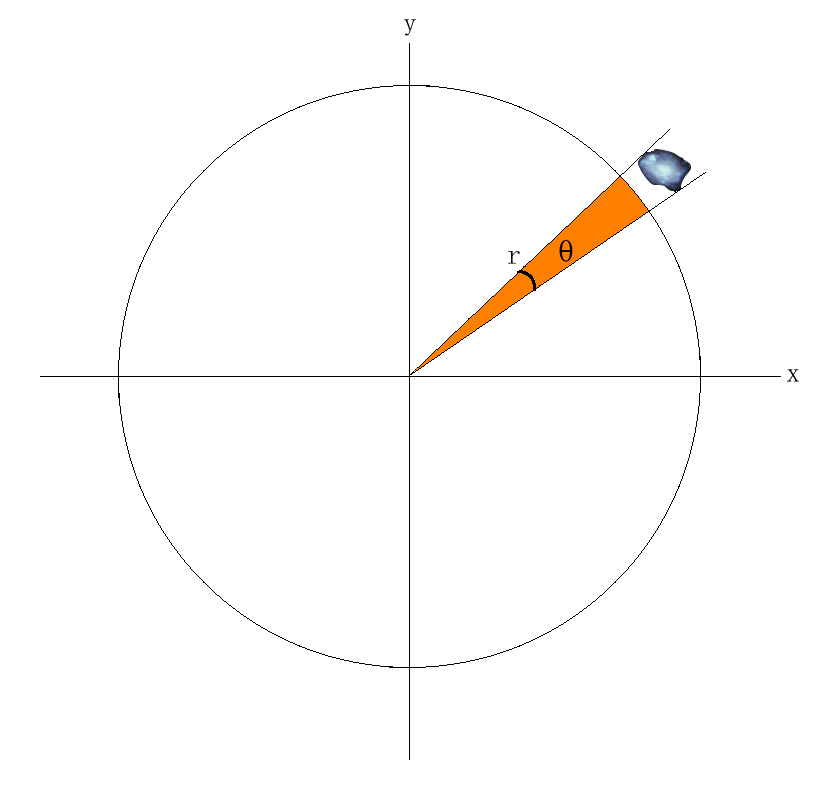
1. We know that the angular size of a distant object is rather small and that it is some fraction of the circle explained above. The measure d shown below represents the physical size of the astrophysical object of interest. Note that the length of the perimeter of the circle is called the circumference, and is defined as,
$$circumference=2\,\pi\,r.\:\:\:\left(1\right)$$
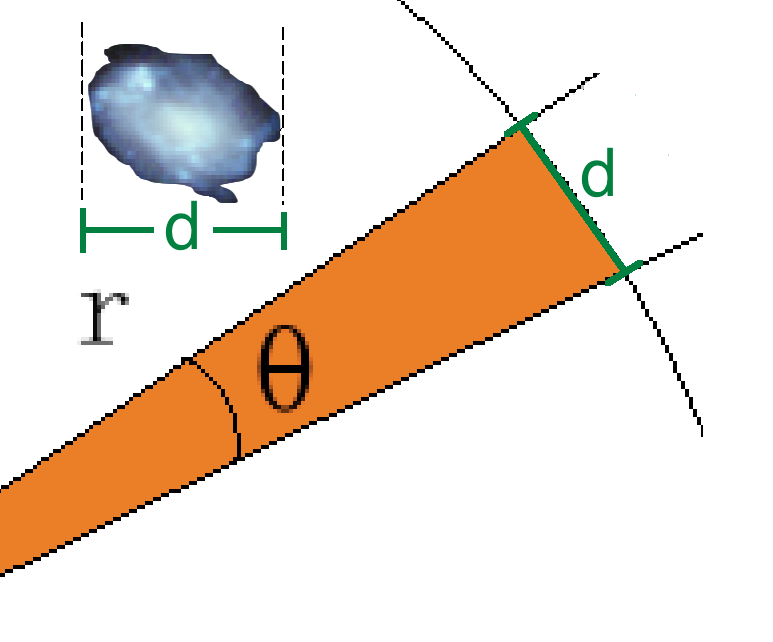
2. Also, since the angle is so small, the actual size of the galaxy, d, is essentially the same as the length of that portion of arc of the circle. Now we can set up a simple ratio since the angular size of the galaxy is to 360 degrees of the circle as the length d is to the circumference of the circle,
$$\frac{\theta\left[degrees\right]}{360^{\circ}}=\frac{d}{2\,\pi\,{r}}.\:\:\:\left(2\rm{a}\right)$$
3. Before moving on, let us rearrange equation (2a) by solving for d/r as,
$$\frac{2\,\pi\,{\theta}\left[degrees\right]}{360^{\circ}}=\frac{d}{r}.\:\:\:\left(2\rm{b}\right)$$
4. Now typically angular sizes are given in units of arcseconds, so we will convert θ into degrees from arcseconds. Since there are 60 arcminutes in 1 degree and 60 arcseconds in one arcminute, we can change the units of θ as follows;
$$\theta\left[degrees\right]=\;\theta\left[arcseconds\right]\times\frac{1\;arcminute}{60\;arcseconds}\times\frac{1\;degree}{60\;arcminutes}.\:\:\:\left(3\right)$$
Now we can substitute equation (3) into (2b) to get a much more compact and usable form that goes as,
$$\frac{d}{r}=\frac{2\,\pi\,{\theta}\left[arcseconds\right]}{\frac{60\;arcseconds}{1\;arcminute}\times\frac{60\;arcminutes}{1\;Degree}\times{360^{\circ}}}\simeq$$$$\simeq\frac{\theta\left[arcseconds\right]}{206,265\;arcseconds}.\:\:\:\left(4\right)$$
Let us try an example where we know the physical size of a galaxy, but not its distance...

We know that a galaxy of this particular type has a diameter of 200,000 light-years. If we know the angular size of the galaxy on the sky is 5 arcseconds, we can determine its distance from earth as follows:
With a little bit of algebra we can solve for r in equation (4), which is the distance to the galaxy. We find that the distance (r) is,
$$r=\frac{d\times206,265\;arcseconds}{\theta\left[arcseconds\right]}\simeq$$$$\simeq\frac{\left(200,000\;lightyears\right){206,265^{\prime\prime}}}{5^{\prime\prime}}lightyears=8.25\times10^9\:lightyears\;\rm{away}.\:\:\:\left(5\right)$$
We can rewrite our distance/angle equation in slightly more simple terms as follows,
$$r\times\theta\left[arcseconds\right]=206,265^{\prime\prime}\times{d}.\:\:\:\left(6\right)$$
You can use this technique to measure distances or sizes as long as you know two of the three variables seen in equation (2) or the more simplified equation (6).
Measuring distances to astrophysical objects is, in general, a tricky business that depends greatly on the scale of the distance you wish to know (See the Cosmic Distance Scale page). For stars that are close by we can use a method known as stellar parallax. Stellar parallax is a method of measuring the distance to nearby sears by using straightforward geometry. If we wish to know the distance to a close star all we need to do (in theory) is observe it two times in one year separated by 6 months (Viewpoint A and Viewpoint B in the diagram below). Since we know the distance from the earth to the sun, our triangle has a base that is two times this distance. The angle φ is measured by looking at how the star of interest shifts in the sky when compared to stars at a much further distance, which appear to remain fixed. (The reason the figure shows an angle of 2φ is because our convention is to assign φ to the angle subtended by the radius of the Earth's orbit around the Sun ("R" in the figure) rather than the angle subtended by the diameter as indicated.) This technique is powerful because it is a direct measure of distance to a star, but is limited by how well we can detect the apparent shift of a star against the background field of stars. This minimum detectable shift sets the furthest distance that can be measured using this technique, since as objects get farther away the apparent shift, φ, decreases.
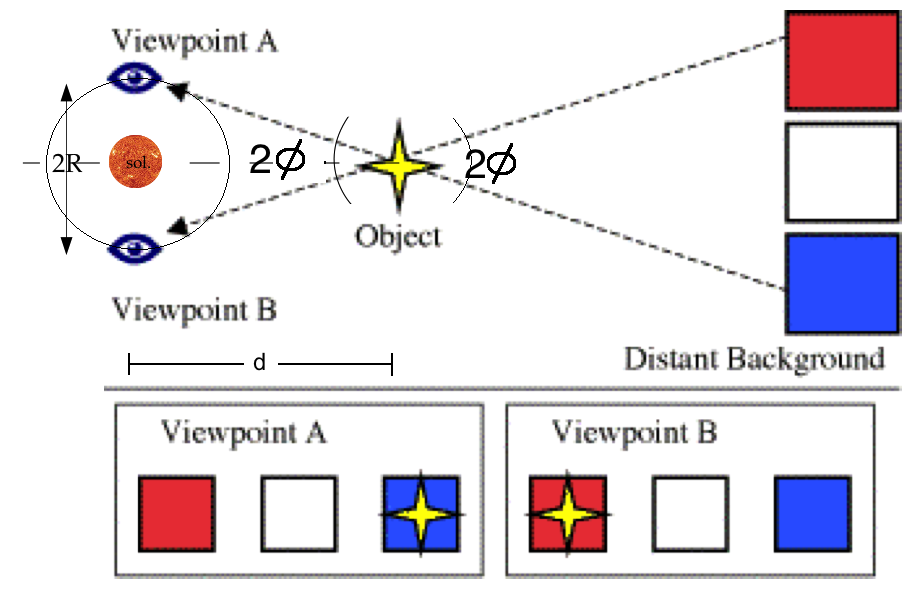
The equation for measuring these distances, d, is quite simple and defines the unit of distance known as the parsec as follows:
$$d[parsecs]=\frac{1}{\phi[arcseconds]}.\:\:\:\left(6\right)$$
Note that the angle φ must be in units of arcseconds, not degrees, if we want to get the distance in parsecs, where 1 parsec = 206,265 Astronomical Units (AUs) ~ 3.3 light-years ~ 3.1×1013 kilometers ~ 1.9×1013 miles . Thus 1 parsec is the distance that would be obtained by measuring a parallax of 1 arcsecond, using a baseline of the Earth-Sun distance (which in turn defines 1 Astronomical Unit). The total angular displacement for such an object over the 6 month span depicted above would be, naturally, 2 arcseconds. Note the even the nearest star to us has a parallax of less than 1 arcsecond.