Padé Approximants

Supporse we are given a power series $ \sum_{i=0}^{\infty }c_{i}z^{i},$ representing a function $ f(z)$, so that

$\displaystyle f(z)=\underset{i=0}{\overset{\infty }{\sum }}c_{i}z^{i}$ (1)

A pade approximant is a rational fraction

$\displaystyle \lbrack L/M]=\frac{a_{0}+a_{1}z+\cdots +a_{L}z^{L}}{b_{0}+b_{1}+\cdots b_{M}z^{M}}$ (2)

which has a Maclaurin expansion which agrees with [*] as far as possible.

Notice that in [*] there are $ L+1$ numerator coefficients and $ M+1$denominator coefficients. There is irrelevant common factor between them $ %% b_{0\text{ }}$

which we take for definiteness equal to one. Hence we have $ L+M+1$unknown coefficients in all. This number suggests that normally the $ [L/M]$ ought to fit the power series [*] through the orders $ 1,z,z^{2},...,z^{L+M}$. In the notation of formal power series,

$\displaystyle \underset{i=0}{\overset{\infty }{\sum }}c_{i}z^{i}=\frac{a_{0}+a_{1}z+\cdots +a_{L}z^{L}}{b_{0}+b_{1}+\cdots b_{M}z^{M}}+O(z^{L+M+1}).$ (3)

Example

$\displaystyle f(z)=1-\frac{1}{2}z+\frac{1}{3}z^{2}+\cdots .$    


$\displaystyle \lbrack 1/0]$ $\displaystyle =$ $\displaystyle 1-\frac{1}{2}z=f(z)+O(z^{2}),$  
$\displaystyle \lbrack 0/1]$ $\displaystyle =$ $\displaystyle \frac{1}{1+\frac{1}{2}z}=f(z)+O(z^{2}),$  
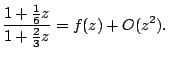$\displaystyle \lbrack 1/1]$ $\displaystyle =$ $\displaystyle \frac{1+\frac{1}{6}z}{1+\frac{2}{3}z}=f(z)+O(z^{2}).$  

Returning to [*] and cross-multiplying, we find that


$\displaystyle (b_{0}+b_{1}+\cdots +b_{M}z^{M})(c_{0}+c_{1}+\cdots )$   $\displaystyle =$ (4)
    $\displaystyle a_{0}+a_{1}z+\cdots +a_{L}z^{L}+O(z^{L+M+1}) \notag$ (5)

Equating the coefficients of $ z^{L+1},z^{L+2},\ldots ,z^{L+M},$ we find


$\displaystyle b_{M}c_{L-M+1}+b_{M-1}c_{L-M+2}+\cdots +b_{0}c_{L+1}$ $\displaystyle =$ $\displaystyle 0,$ (6)
$\displaystyle b_{M}c_{L-M+2}+b_{M-1}c_{L-M+3}+\cdots +b_{0}c_{L+2}$ $\displaystyle =$ $\displaystyle 0, \notag$ (7)
    $\displaystyle \vdots \notag$ (8)
$\displaystyle b_{M}c_{L}+b_{M-1}c_{L+1}+\cdots +b_{0}c_{L+M}$ $\displaystyle =$ $\displaystyle 0. \notag$ (9)

For consistency we define $ c_{j}=0$ if $ j<0$. Since $ b_{0}=1,$Eqs. [*] becomes a set of $ M$ linear equations for the $ M$ unknown denominator coefficients:


\begin{displaymath}\left[ \begin{array}{lllll} c_{L-M+1} & c_{L-M+1} & c_{L-M+1}... ...\\ b_{M-1} \\ b_{M-2} \\ \vdots \\ b_{1} \end{array}\right]\end{displaymath}   $\displaystyle =$ (10)
    \begin{displaymath}-\left[ \begin{array}{l} c_{L+1} \\ c_{L+2} \\ c_{L+3} \\ \vdots \\ c_{L+M} \end{array}\right] , \notag\end{displaymath} (11)

from which the $ b_{i}$ may be found. The numerator coefficients, $ %% a_{0,}a_{1},\ldots ,a_{L}$ , follow from [*] by equating the coefficients $ 1,z,z^{2},\ldots ,z^{L}$:


$\displaystyle a_{0}$ $\displaystyle =$ $\displaystyle c_{0}$ (12)
$\displaystyle a_{1}$ $\displaystyle =$ $\displaystyle c_{1}+b_{1}c_{0}, \notag$ (13)
$\displaystyle a_{2}$ $\displaystyle =$ $\displaystyle c_{2}+b_{1}c_{1}+b_{2}c_{0}, \notag$ (14)
    $\displaystyle \vdots \notag$ (15)
$\displaystyle a_{L}$ $\displaystyle =$ $\displaystyle c_{L}+\overset{\min (L,M)}{\underset{i=1}{\sum }}b_{i}c_{L-i}. \notag$ (16)


Thus from [*] and [*] we determine the Pade numerator and denominator and these equations are called the pade equations; we have obtained an $ [L/M]$ Pade approximant which agrees with $ \sum_{i=0}^{\infty }c_{i}z^{i}$ through order $ z^{L+M}.$

Given the power series, [*] and [*] show how the Pade approximants are constructed, but it is important to distinguish between problems of convergence of Pade approximants and problems of their construction: we do not need to know about the existence of any function $ f(z)$ with $ %% \sum_{i=0}^{\infty }c_{i}z^{i}$ as its Maclauring series.

The self-energy $ \Sigma (i\omega _{n})$ and Green function $ G(i\omega _{n})$ are calculated at the imaginary Matsubara frequencies $ i\omega _{n}=i\pi (2n+1)/\beta $ . It is enough to calculate expectation values, such as orbital occupancies $ n$ , but in order to calculate spectral properties one need to know Green function on the real axis. The real axis variant of equations is much more complicated and hard to implement numerically than Matsubara frequencies version. It is much more convenient to perform analytical continuation from imaginary energy values to the real ones. For such continuation we have used Padé approximant algorithm. If one has a set of the complex energies $ z_{i}$ $ (i=1,...,M)$ and the set of values of the analytical function $ u_{i}$ , then the approximant is defined as continued fraction:

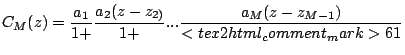$\displaystyle C_{M}(z)=\frac{a_{1}}{1+}\frac{a_{2}(z-z_{2)}}{1+}...\frac{a_{M}(z-z_{M-1})}{<tex2html_comment_mark>6 1}$ (17)

where the coefficients $ a_{i}$ are to be determined so that:

$\displaystyle C_{M}(z_{i})=u_{i,}\ i=1,...,M$ (18)

The coefficients $ a_{i}$ are then given by the recursion:
$\displaystyle a_{i}$ $\displaystyle =$ $\displaystyle g_{i}(z_{i}),\ g_{1}(z_{i})=u_{i},\;i=1,...,M$ (19)
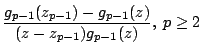$\displaystyle g_{p}(z)$ $\displaystyle =$ $\displaystyle \frac{g_{p-1}(z_{p-1})-g_{p-1}(z)}{(z-z_{p-1})g_{p-1}(z)}%% ,\;p\geq 2$ (20)

The recursion formula for continued fraction finally yields:

$\displaystyle C_{M}(z)=A_{M}(z)/B_{M}(z)$ (21)

where
$\displaystyle A_{n+1}(z)$ $\displaystyle =$ $\displaystyle A_{n}(z)+(z-z_{n})a_{n+1}A_{n-1}(z) \notag$ (22)
$\displaystyle B_{n+1}(z)$ $\displaystyle =$ $\displaystyle B_{n}(z)+(z-z_{n})a_{n+1}B_{n-1}(z)$ (23)

and

$\displaystyle A_{0}=0,\;A_{1}=a_{1},\;B_{0}=B_{1}=1$    



Vidberg H.J. and Serene J.W., Journal of Low Temperature Physics, v 29, 179 (1977)


Viktor Oudovenko 2001-04-22