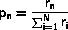
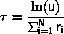
where u is a random number uniformly distributed in the interval [0,1[.
The kinetic Monte Carlo algorithm allows us to simulate the behaviour based on the microscopic kinetics.
The KMC algorithm is as follows:
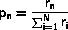
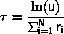
In our mechanism the possible events are the desorption of a A2*-molecule and the diffusion of A2* or A* to a neighbor site.
Usually the events are enumerated by looping over the sites in the lattice and one must be careful to list each event exactly once.
In the following we will need an algorithm to select a number, n,
out of N with weight Wn or, equivalently, probability
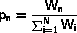
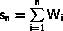
During the simulation the temperature increases.
Frequently this implies that the surface diffusion will go from
slow to extremely fast.
If we ignore this complication, the simulation will start with reasonably
large timesteps, say  =1 s.
As the temperature increases, the diffusion rate increases,
=1 s.
As the temperature increases, the diffusion rate increases,
 decreases
and the algorithm gradually becomes intolerably slow, say
decreases
and the algorithm gradually becomes intolerably slow, say  =1 ns.
=1 ns.
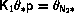
When the KMC algorithm is formulated as in ? increasing to infinity the rate of one of the steps in the mechanism leads to a dramatical increase in the computational effort rather than a fast approach to equilibrium.
The large but smooth increase in diffusion rate with temperature implies that simple approximations, such as treating the diffusion as either slow or fast independent of the temperature, will not work.
Fortunately, a smooth transtion to fast diffusion can easily be implemented by a slight modification of the KMC algorithm.
We decide on a limit between fast and slow diffusion events and then perform two scans over the system.
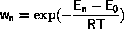
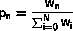
In some cases an atom cannot move by any fast reaction, e.g because all its neighbor sites are occupied. It is not required to implement this as a special case. If the atom cannot move by any fast reaction, the set consists of only the current site of the atom. This site then has p0=1 and is selected with probability 1.
The first scan consider only fast reactions and contributes significantly to the approach to equilibrium, but does not propagate the system in time.
The second scan propagates the system in time in accordance with equation ?.