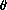(*|A2*)
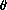A2*
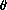(A*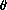|A*)
A*
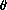A2*
is the probability a site is occupied by
A2*,
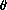(*|A2*)
is the conditional probability
that one of its neighbor sites is free.
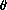A*
is the probability a site is occupied by
A* and
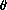(A*|A*)
is the conditional probability that one of
its neighbor sites is occupied by A*.
When the rate equation is integrated using Runge-Kutta methods, the coverages are interpreted as the coverage averaged for the surface as a whole.
If the coverages on neighbor sites are independent the exact rate equation is identical to the mean-field rate equation.
The exact rate equation talks of the coverage probabilities for individual sites and the evolution in time cannot be expressed in closed form. However, it is well known, at least to chemists, that the mean field equation is almost always a fairly good approximation to the exact equation. The reason is that stability in the presence of fluctuations and independence of the equilibrium composition on the size of the system put severe constraints on the functional form of the rate equation.
It is interesting that for adsorption of surfaces there are some cases where this approximation is poor.
In the model
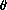(A*|A*) may be
much larger than 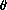(A*)
simply because the two
A-atoms formed by
dissociation of one A2 molecule remain neighbors.
Even if the diffusion is fast,
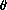(A*|A*) can be much larger than
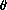A*
if there is an attractive interaction between adsorbed A-atoms
and much smaller if there is a repulsive interaction.