


Next: References
Up: Toward a Symmetrization of
Previous: The Interaction Strength and
A repelling force has obvious applicability toward observational cosmology. If we consider a dust filled universe, with no density gradients
in 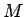 or
or
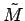 , we ought to be able to approximate the observed Hubble flow in a simple fashion. The repelling field on a shell of material, due to
the presence of
, we ought to be able to approximate the observed Hubble flow in a simple fashion. The repelling field on a shell of material, due to
the presence of
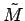 interior to the shell, will be:
interior to the shell, will be:
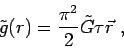 |
(9) |
where 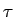 is the 4-dimensional volume density of the
is the 4-dimensional volume density of the
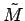 . (This result follows from the fact that the hyper-volume of the sphere of
. (This result follows from the fact that the hyper-volume of the sphere of
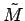 is:
is:
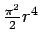 ). Thus, our interaction superficially has the same effect as
the cosmological constant, whereby:
). Thus, our interaction superficially has the same effect as
the cosmological constant, whereby:
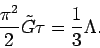 |
(10) |
Using the results of Perlmutter et al. (1999) and
Riess et al. (1998), we set
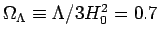 , and therefore find (with
, and therefore find (with
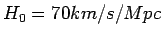 ) :
) :
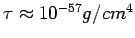 .
We are now afforded another consistency check with regard to our original
assumption of equal mass distributions of M and
.
We are now afforded another consistency check with regard to our original
assumption of equal mass distributions of M and
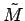 over 100 Mpc. Using the
4 dimensional volume for
over 100 Mpc. Using the
4 dimensional volume for
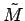 , we find that
, we find that
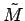
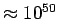 g. If we assume that the average 3-D density of real matter is given by
g. If we assume that the average 3-D density of real matter is given by
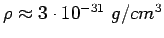 for the M (i.e. there is no
``dark" matter), we get
for the M (i.e. there is no
``dark" matter), we get
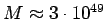 g.
However, since the cosmological principle implies that expansion proceeds in the same way for all shells, we see that
g.
However, since the cosmological principle implies that expansion proceeds in the same way for all shells, we see that
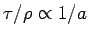 , where
, where 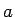 is the scale factor for the expansion. Thus, the repulsive stress is diluted over time (unlike the stress due to a
is the scale factor for the expansion. Thus, the repulsive stress is diluted over time (unlike the stress due to a 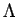 term), and therefore the acceleration may end at some time in the future, thereby avoiding the problems
that a vacuum dominated, eternally accelerating universe faces (see Barrow, Bean and Magueijo, 2000).
term), and therefore the acceleration may end at some time in the future, thereby avoiding the problems
that a vacuum dominated, eternally accelerating universe faces (see Barrow, Bean and Magueijo, 2000).
We would like to thank Tad Pryor, Jerry Sellwood, Jim Peebles, John Conway, Arthur Kosowsky, Tina Kahniashvili, Stu Kurtz, Libby Maljian
and Stacy McGaugh for stimulating discussions, and Patty Gulyas for help in the manuscript preparation.



Next: References
Up: Toward a Symmetrization of
Previous: The Interaction Strength and
Terry Matilsky
![]() or
or
![]() , we ought to be able to approximate the observed Hubble flow in a simple fashion. The repelling field on a shell of material, due to
the presence of
, we ought to be able to approximate the observed Hubble flow in a simple fashion. The repelling field on a shell of material, due to
the presence of
![]() interior to the shell, will be:
interior to the shell, will be: