Since ![]() has a different dimensionality than G, we can now use it
instead of G, to form the standard units of m, r, and t by combining
has a different dimensionality than G, we can now use it
instead of G, to form the standard units of m, r, and t by combining
![]() with h and c. So doing yields:
with h and c. So doing yields:
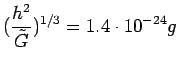 |
|||
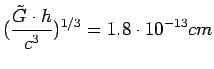 |
|||
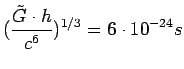 |
(6) |
Another interesting result is obtained when the classical electrostatic force
is equated with the ![]() interaction at the distance
interaction at the distance ![]() , using
, using ![]() as one
of the masses,
and solving for the other mass. We get:
as one
of the masses,
and solving for the other mass. We get:
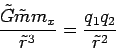 |
(7) |
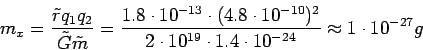 |
(8) |
This, of course, is very close to the value for the electron's rest mass.
Thus, we apparently have a way to uniquely determine both the proton and
electron rest masses. While these results could be considered as merely chance
numerical coincidences, it is possible that this result could point toward some sort of exchange interaction, whereby quantum mechanical operators allow interchanges between fundamental M and
![]() ``particles".
``particles".