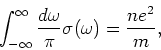f-sum rule
The retarded current-current correlation function is defined by
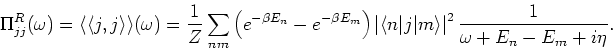 |
(1) |
The corresponding spectral function is
In terms of the spectral function, the real part of the conductivity (which
is what enters the f-sum rule) is given by,
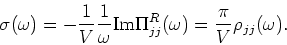 |
(3) |
We define the polarization operator 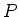 such that
such that
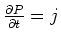 .
Then,
.
Then,
where
![\begin{displaymath}
\rho_{Pj} (\omega ) = \int_{- \infty}^{\infty} \frac{dt}{2 \pi} e^{i \omega t} \langle
[ P(t), j ] \rangle .
\end{displaymath}](img13.gif) |
(5) |
Then,
The current operator is given by
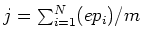 , where
, where 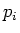 is the momentum of the i-th particle. The polarization operator is given by
is the momentum of the i-th particle. The polarization operator is given by
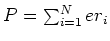 , where
, where 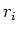 is the position of the i-th particle.
Since,
is the position of the i-th particle.
Since,
(in units where 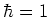 ), we finally get the f-sum rule as
), we finally get the f-sum rule as
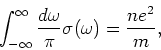 |
(7) |
where 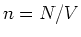 is the density of particles.
is the density of particles.
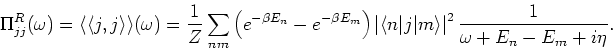
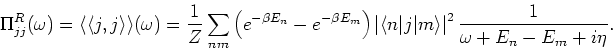
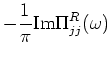
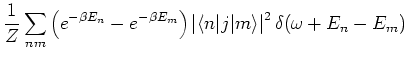
![$\displaystyle \int_{- \infty}^{\infty} \frac{dt}{2 \pi} e^{i \omega t} \langle [ j(t) , j] \rangle .$](img6.gif)
![$\displaystyle \int_{- \infty}^{\infty} \frac{dt}{2 \pi} e^{i \omega t}
\langle [ \frac{\partial P}{\partial t}, j ] \rangle$](img10.gif)
![$\displaystyle - i \omega \int_{- \infty}^{\infty} \frac{dt}{2 \pi} e^{i \omega t} \langle [ P(t),
j ] \rangle$](img11.gif)
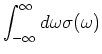
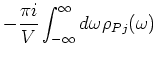
![$\displaystyle - \frac{\pi i}{V} \langle [P(0), j ] \rangle .$](img16.gif)
![\begin{displaymath}[P, j]= \frac{e^2}{m} \sum_{ij} [ r_i , p_j] = \frac{N e^2 i}{m},
\end{displaymath}](img21.gif)