We consider impurity electrons on a single site hybridizing with a bath of
conduction electrons. The electrons carry ![]() spin. We consider the
limiting case where the on-site Coulomb repulsion (
spin. We consider the
limiting case where the on-site Coulomb repulsion (![]() ) at the impurity site
is infinitely large. Thus, at most a single electron can occupy the impurity
site (multiple occupancy is not allowed). In this limit, the allowed states
of the impurity site are
) at the impurity site
is infinitely large. Thus, at most a single electron can occupy the impurity
site (multiple occupancy is not allowed). In this limit, the allowed states
of the impurity site are ![]() (i.e., no electron), and
(i.e., no electron), and ![]() where
where
![]() (i.e., a single electron with
(i.e., a single electron with ![]() spin
spin ![]() ). The
Hubbard operators are defined as
). The
Hubbard operators are defined as
![]() , where
, where
![]() . In this restricted subspace creation operator for an
impurity electron
. In this restricted subspace creation operator for an
impurity electron
![]() . Similarly,
. Similarly,
![]() . The completeness relation in this subspace (of the impurity
level) is given by
. The completeness relation in this subspace (of the impurity
level) is given by
![]() . Note, that the Hubbard
operators satisfy the relation
. Note, that the Hubbard
operators satisfy the relation
![]() . This is unlike standard commutation or anticommutation
of bosons and fermions. The Hamiltonian for the system is given by
. This is unlike standard commutation or anticommutation
of bosons and fermions. The Hamiltonian for the system is given by
where
We consider the retarded Green's function
![]() . The corresponding spectral function
is given by
. The corresponding spectral function
is given by
The first moment is given by
![]() . We can write
. We can write
![]() , where
, where
![]() is the expectation of electron occupancy at the
impurity site. Also,
is the expectation of electron occupancy at the
impurity site. Also,
![]() . Thus,
. Thus,
| (1) |
the first moment gives the total spectral weight of the f-band.
For the calculation of the second moment we get
Then,
![\begin{displaymath}
\langle \{ [ {\mathcal H}, X_{0n} ] , X_{n0} \} \rangle = - ...
...eq n} V^{\ast}_{{\bf k}} \langle c_{{\bf k}m} X_{m0} \rangle .
\end{displaymath}](img26.gif) |
(2) |
| (3) |
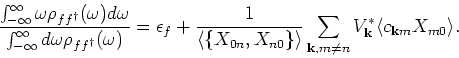
Presumably (since we cannot conclusively say anything about the line shape) the spectral function is peaked at this energy. The second term is the shift in the energy of the f-level due to hybridization.
For the third moment we get
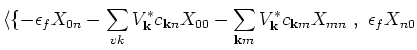 |
|||
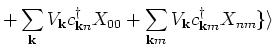 |
|||
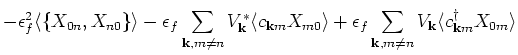 |
|||
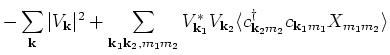 |
|||
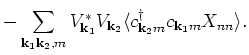 |
(4) |
We can show that
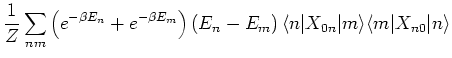 |
|||
| (5) |
This is due to time translation invariance of the correlation function in equilibrium. Using this result we get,
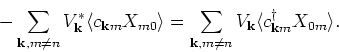 |
(6) |
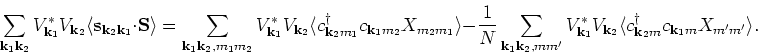 |
(7) |
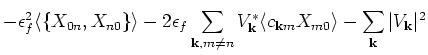 |
|||
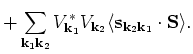 |
(8) |
We identify the last term in the above equation as a spin-spin correlation function. The sum rule for the third moment is given by
| (9) |
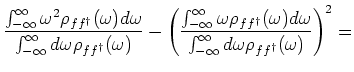 | |||
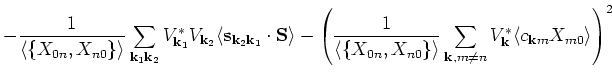 |
(10) | ||
Originally the f-level was a delta function peak at
The retarded current-current correlation function is defined by
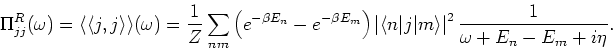 |
(11) |
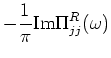 |
|||
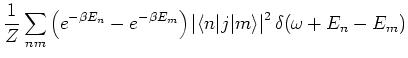 |
|||
![$\displaystyle \int_{- \infty}^{\infty} \frac{dt}{2 \pi} e^{i \omega t} \langle [ j(t) , j] \rangle .$](img56.gif) |
(12) |
In terms of the spectral function, the real part of the conductivity (which is what enters the f-sum rule) is given by,
| (13) |
![$\displaystyle \int_{- \infty}^{\infty} \frac{dt}{2 \pi} e^{i \omega t}
\langle [ \frac{\partial P}{\partial t}, j ] \rangle$](img60.gif) |
|||
![$\displaystyle - i \omega \int_{- \infty}^{\infty} \frac{dt}{2 \pi} e^{i \omega t} \langle [ P(t),
j ] \rangle$](img61.gif) |
|||
| (14) |
where
| (15) |
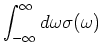 |
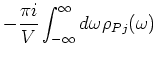 |
||
![$\displaystyle - \frac{\pi i}{V} \langle [P(0), j ] \rangle .$](img66.gif) |
(16) |
The current operator is given by
![\begin{displaymath}[P, j]= \frac{e^2}{m} \sum_{ij} [ r_i , p_j] = \frac{N e^2 i}{m},
\end{displaymath}](img71.gif)
(in units where
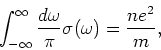 |
(17) |