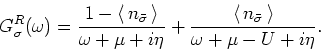- To calculate the retarded Green's function and the spectral function we will
first calculate the temperature Green's function and then take appropriate
analytic continuation.
The temperature Green's function is defined as,
The Fourier transform in terms of fermionic Matsubara frequency
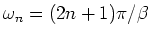 , is
, is
Since,
we get from equations (3) and (4),
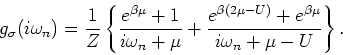 |
(5) |
Then, after the analytic continuation
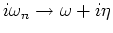 ,
we have,
,
we have,
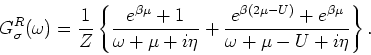 |
(6) |
The spectral function is given by,
In the non-interacting case the spectral function has a single pole with
weight one, i.e,
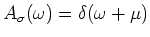 . The effect of interaction
is to produce two poles with finite energy gap
. The effect of interaction
is to produce two poles with finite energy gap 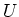 . The total spectral weight,
which is always one, is shared between the two poles.
. The total spectral weight,
which is always one, is shared between the two poles.
- The Hubbard operators are defined as
Their conjugate operators are repectively,
Now, it is easy to see that
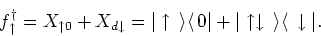 |
(10) |
- Similarly, we have,
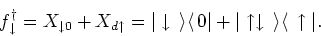 |
(11) |
- The anticommutator
since
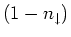 is either zero or one.
Thus,
is either zero or one.
Thus,
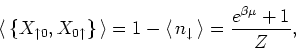 |
(13) |
is the average occupation of a 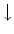 -hole. We also note, from equation (7),
that this is also the spectral weight for the pole corresponding to single
occupancy.
-hole. We also note, from equation (7),
that this is also the spectral weight for the pole corresponding to single
occupancy.
Similarly, the anticommutator
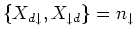 . Thus,
. Thus,
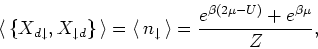 |
(14) |
is the average occupation of a 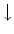 -electron. Again from equation (7) we
note that this is the spectral weight for the pole corresponding to double
occupancy.
-electron. Again from equation (7) we
note that this is the spectral weight for the pole corresponding to double
occupancy.
- To evaluate the commutator
![$[{\mathcal H}, X_{0\uparrow }]$](img49.gif) , it is enough to consider the
state
, it is enough to consider the
state
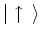 , since all other states give zero when acted on by
, since all other states give zero when acted on by
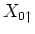 . We have
. We have
![$[{\mathcal H}, X_{0\uparrow }] \vert \uparrow {\,\rangle }= \mu \vert 0 {\,\rangle }= \mu X_{0\uparrow }
\vert \uparrow {\,\rangle }$](img51.gif) . Thus,
. Thus,
![$[{\mathcal H}, X_{0\uparrow }] = \mu X_{0\uparrow }$](img52.gif) , and
, and
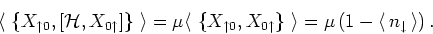 |
(15) |
Comparing with equation (7) we find that the energy coefficient in the above
expression gives the pole for the singly occupied state.
Similarly, we can show that
![$[{\mathcal H}, X_{\downarrow d}] = (\mu - U) X_{\downarrow d}$](img54.gif) , and
, and
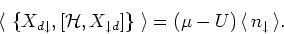 |
(16) |
Here the energy coefficient gives the pole for the doubly occupied state.
- Comment
To put parts (1), (4) and (5) into proper perspective we will re-evaluate the
retarded Green's function using the Hubbard operators. From definition,
Here 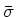 is the spin opposite to
is the spin opposite to 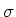 . In the last line above, we have
used the fact that cross-terms are zero. Now, from our discussion in part (5),
we know that
. In the last line above, we have
used the fact that cross-terms are zero. Now, from our discussion in part (5),
we know that
![$[{\mathcal H}, X_{0\sigma }] = \mu X_{0\sigma }$](img62.gif) and that
and that
![$[{\mathcal H}, X_{\bar{\sigma}d}] =
(\mu - U) X_{\bar{\sigma}d}$](img63.gif) . Then,
. Then,
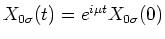 , and
, and
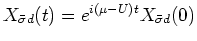 . We can write,
. We can write,
From our discussion in part (4) we know that
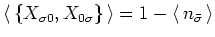 and that
and that
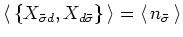 . So, finally we have,
. So, finally we have,
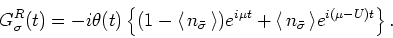 |
(17) |
Taking the Fourier transform of the above equation we get,
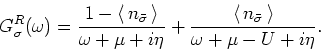 |
(18) |
This is nothing but equation (6) in a more compact form.
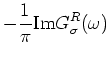
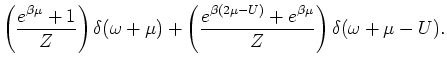
![]() . Thus,
. Thus,
![]() , and
, and