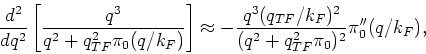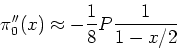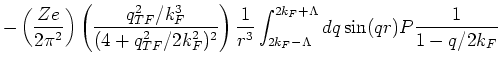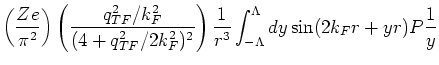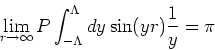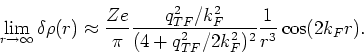Screening of an Impurity Charge: Friedel Oscillations
We want to study the response of an electron gas to a static impurity with
charge 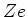 . At the level of random phase approximation, the change in the
electron distribution induced by the impurity charge is given by
. At the level of random phase approximation, the change in the
electron distribution induced by the impurity charge is given by
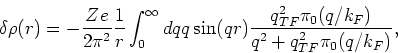 |
(1) |
where 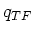 is the Thomas-Fermi screening length, and
is the Thomas-Fermi screening length, and 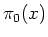 is the
Lindhard function for density-density correlation and is given by
is the
Lindhard function for density-density correlation and is given by
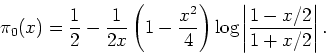 |
(2) |
We note that the above function is non-analytic at 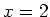 . This is due to low
energy electron-hole excitations in a degenerate electron gas at wave-vector
. This is due to low
energy electron-hole excitations in a degenerate electron gas at wave-vector
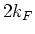 . These processes are important in screening the impurity charge, and
they give rise to the Friedel oscillations. The regular part of the integral
in equation (1) gives the usual Thomas-Fermi screening, which has the
asymptotic (
. These processes are important in screening the impurity charge, and
they give rise to the Friedel oscillations. The regular part of the integral
in equation (1) gives the usual Thomas-Fermi screening, which has the
asymptotic (
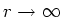 ) form
) form
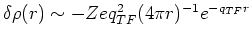 . In this exercise
we will calculate only the irregular part of the integral in equation (1)
which shows the Friedel oscillations. After two partial integrals we get
. In this exercise
we will calculate only the irregular part of the integral in equation (1)
which shows the Friedel oscillations. After two partial integrals we get
We will keep track of the most singular term which is
with
around 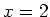 . Close to
. Close to 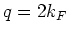 we get,
we get,
where 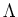 is a finite cut-off. The integrand
is a finite cut-off. The integrand
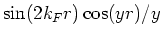 drops out because it is odd over the range of integration. We also have
drops out because it is odd over the range of integration. We also have
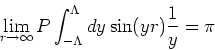 |
(5) |
for any finite 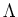 . Using these results we get
. Using these results we get
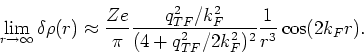 |
(6) |
![]() . At the level of random phase approximation, the change in the
electron distribution induced by the impurity charge is given by
. At the level of random phase approximation, the change in the
electron distribution induced by the impurity charge is given by
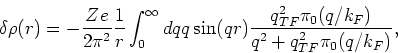
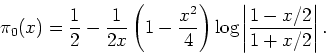
![$\displaystyle \frac{Ze}{2 \pi^2} \frac{1}{r^3} \int_0^{\infty } dq \sin(qr)
\frac{d^2}{d q^2} \left[ \frac{q q_{TF}^2 \pi_0}{q^2 + q_{TF}^2 \pi_0} \right]$](img12.gif)
![$\displaystyle - \frac{Ze}{2 \pi^2} \frac{1}{r^3} \int_0^{\infty } dq \sin(qr)
\frac{d^2}{d q^2} \left[ \frac{q^3}{q^2 + q_{TF}^2 \pi_0 (q/k_F)} \right].$](img13.gif)