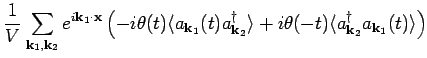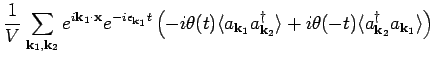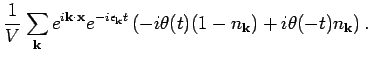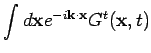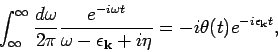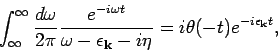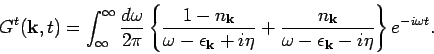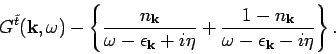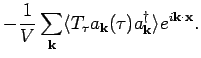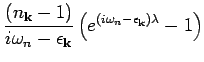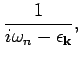Solution to Exercise 17
We want to evaluate various Green's functions for a system of free fermions
described by the Hamiltonian
We will understand operator averages by
Then, from quantum statistical mechanics we can show that
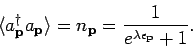 |
(1) |
In the following we will use the Fourier transform of the field operators,
which are defined as
Here 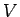 is the volume of the system. For a non-interacting system, the time
evolution of the operators
is the volume of the system. For a non-interacting system, the time
evolution of the operators
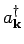 and
and 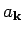 is very simple. We find
that
is very simple. We find
that
Similarly we can show that
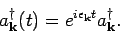 |
(5) |
- The time ordered Green's function is defined as
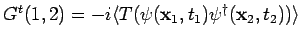 . Since the system is translation
invariant in space and time variables, the Green's function is a function of
. Since the system is translation
invariant in space and time variables, the Green's function is a function of
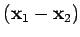 and
and 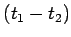 only. So, without any loss of generality
we can put
only. So, without any loss of generality
we can put 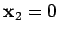 and
and 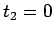 . We can write
. We can write
The Fourier transform of
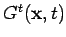 into momentum space gives
into momentum space gives
In the above the first term is for propagation of particle excitation in
forward time, and the second term denotes propagation of hole excitation in
backward time. Next we make use of the identities
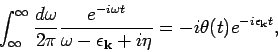 |
(8) |
and
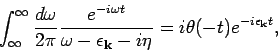 |
(9) |
to write
Thus,
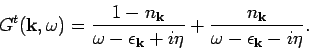 |
(10) |
- The anti-time ordered Green's function defined as
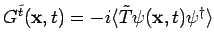 , can be calculated along similar lines. We
get
, can be calculated along similar lines. We
get
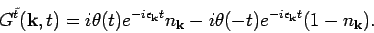 |
(11) |
The Fourier transform into frequency space gives,
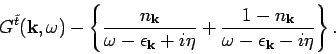 |
(12) |
- The correlation function
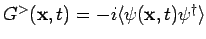 has Fourier
transforms
has Fourier
transforms
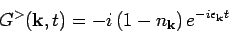 |
(13) |
and
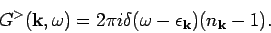 |
(14) |
- For
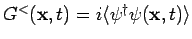 we get
we get
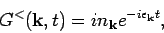 |
(15) |
and
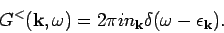 |
(16) |
-
The Fourier transform is
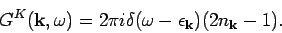 |
(18) |
-
The Fourier transforms are
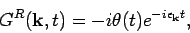 |
(20) |
and
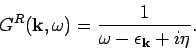 |
(21) |
-
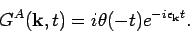 |
(22) |
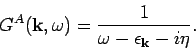 |
(23) |
It is important to note that in the above calculations we have not used the
explicit form of the distribution function 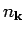 . The form of the
distribution function depends on the density operator, and so the above
results are true for arbitrary density operators. Also note that, unlike
the other functions,
. The form of the
distribution function depends on the density operator, and so the above
results are true for arbitrary density operators. Also note that, unlike
the other functions,
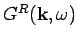 and
and
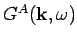 have information only
about the excitation spectrum, but they have no information about the
distribution function
have information only
about the excitation spectrum, but they have no information about the
distribution function 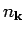 .
.
- The Matsubara Green's function is given by
The evolution in imaginary time is given by
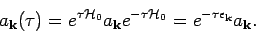 |
(25) |
Then,
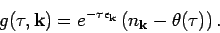 |
(26) |
The principal region where 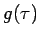 is defined is
is defined is
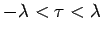 . Over this
region, it can be seen explicitly from the above equation that
. Over this
region, it can be seen explicitly from the above equation that 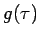 is
antiperiodic, i.e.,
is
antiperiodic, i.e.,
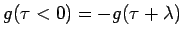 . It is important to note that
this property depends on the explicit form of the distribution function.
Due to the antiperiodicity, the Fourier transform to imaginary frequencies,
. It is important to note that
this property depends on the explicit form of the distribution function.
Due to the antiperiodicity, the Fourier transform to imaginary frequencies,
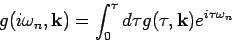 |
(27) |
is nonzero only for
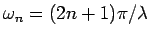 . These are fermionic Matsubara
frequencies. We get,
. These are fermionic Matsubara
frequencies. We get,
because
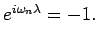
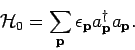
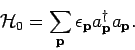
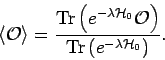
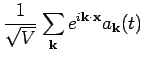
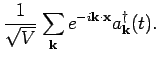
![$\displaystyle a_{{\bf k}} + \left( it \right) \left[ {\mathcal H}_0, a_{{\bf k}...
...ft[ {\mathcal H}_0, \left[ {\mathcal H}_0, a_{{\bf k}} \right]
\right] + \cdots$](img14.gif)