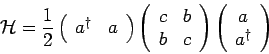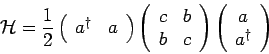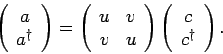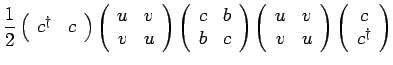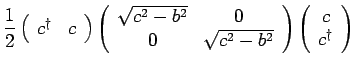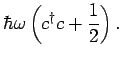Solution to Exercise 16
We want to diagonalize the bosonic Hamiltonian
by appropriate canonical transformation. Here 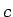 ,
, 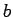 are real and
are real and 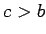 .
The operators obey bosonic commutation relation
.
The operators obey bosonic commutation relation
![$[a, a^{\dagger}] = 1$](img5.gif) .
We consider a transformation of the form
.
We consider a transformation of the form
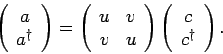 |
(1) |
Inverting the above transformation we get
![$[ c , c^{\dagger}] = 1/ (u^2 - v^2)$](img7.gif) .
Since, the transformation has to be canonical, we get
.
Since, the transformation has to be canonical, we get 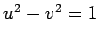 . This is
satisfied by
. This is
satisfied by
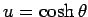 and
and
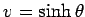 . Thus, the two unknown parameters
have been reduced to one. We will choose this unknown
. Thus, the two unknown parameters
have been reduced to one. We will choose this unknown 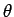 such that the
Hamiltonian is diagonal in terms of the
such that the
Hamiltonian is diagonal in terms of the
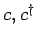 operators. From equation (1)
we get
operators. From equation (1)
we get
The value of 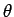 that diagonalizes the Hamiltonian is given by
that diagonalizes the Hamiltonian is given by
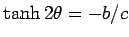 . Then,
. Then,
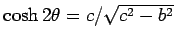 and
and
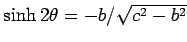 . We get,
. We get,
Thus, the spectrum is the usual harmonic oscillator spectrum with frequency
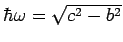 .
.