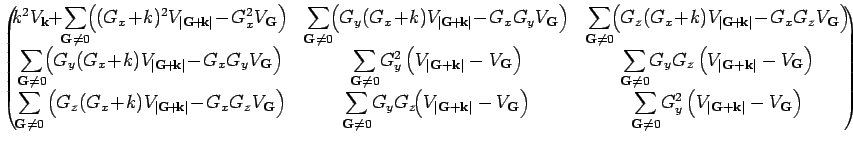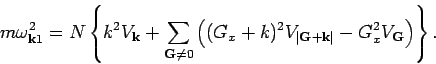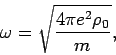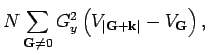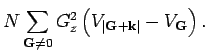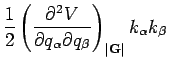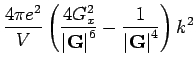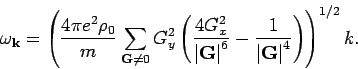Solution to Exercise 15
We consider the Hamiltonian,
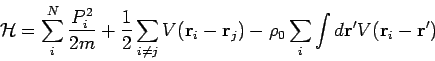 |
(1) |
where 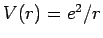 is the Coulomb potential with which the ions interact,
and
is the Coulomb potential with which the ions interact,
and 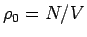 is a uniform background charge for overall neutrality.
To study small oscillations we will expand the potential term (
is a uniform background charge for overall neutrality.
To study small oscillations we will expand the potential term (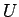 ) in the
Hamiltonian around the equilibrium position of each ion. Let
) in the
Hamiltonian around the equilibrium position of each ion. Let
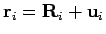 , where
, where 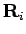 are the equilibrium positions and
are the equilibrium positions and 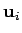 are small
deviations from equilibrium. Expanding upto second order we get,
are small
deviations from equilibrium. Expanding upto second order we get,
The first two terms in the above expansion are constants and they can be
dropped out from the Hamiltonian. The third and fourth terms are zero
because they represent the force on the ions at their equilibrium positions.
Only the second order terms survive, and we can write the Hamiltonian for
lattice vibrations as,
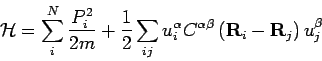 |
(2) |
where
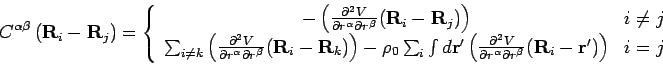 |
(3) |
We expand 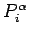 and
and 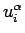 in Fourier series
in Fourier series
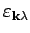 are the polarization vectors. For each wavevector
are the polarization vectors. For each wavevector 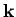 there is one longitudinal direction (
there is one longitudinal direction (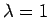 ) and two transverse directions
) and two transverse directions
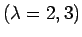 . They define an orthonormal basis for three dimensional vectors.
Thus,
. They define an orthonormal basis for three dimensional vectors.
Thus,
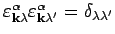 .
Since
.
Since 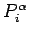 and
and 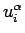 are real quantities, we impose the conditions
are real quantities, we impose the conditions
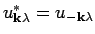 ,
,
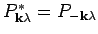 and
and
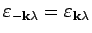 . It is important to note that in the above
Fourier expansion, due to periodicity of the lattice,
. It is important to note that in the above
Fourier expansion, due to periodicity of the lattice,
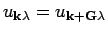 where
where 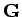 is a reciprocal lattice vector. To avoid redundant
Fourier components we restrict the wavevector
is a reciprocal lattice vector. To avoid redundant
Fourier components we restrict the wavevector 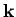 to the first Brillouin
zone (BZ). The same consideration applies for
to the first Brillouin
zone (BZ). The same consideration applies for
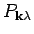 . We also define
the
Fourier transform of the dynamical matrix
. We also define
the
Fourier transform of the dynamical matrix
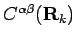 by
by
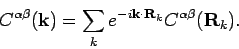 |
(4) |
Here again 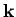 is restricted to the first Brillouin zone.
In terms of the Fourier components the Hamiltonian in equation (2) can be
expressed as
is restricted to the first Brillouin zone.
In terms of the Fourier components the Hamiltonian in equation (2) can be
expressed as
To write the above equation we have used the orthonormality of the
polarization vectors, and the relation
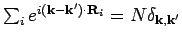 . We can choose the polarization vectors as the
eigenvectors of the dynamical matrix , i.e.
. We can choose the polarization vectors as the
eigenvectors of the dynamical matrix , i.e.
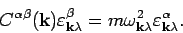 |
(5) |
Then, the Hamiltonian for the phonons can be written as
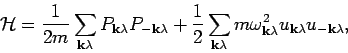 |
(6) |
which describe oscillators whose frequency depend on wavevector. To find the
phonon frequencies we have to solve the eigenvalue equation (5). For this we
have to calculate
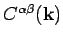 .
We get, from equations (3) and (4)
.
We get, from equations (3) and (4)
In the last line we could add the term 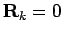 in the summation because it
gives zero contribution to the sum. We express the Fourier transform of the
Coulomb potential by
in the summation because it
gives zero contribution to the sum. We express the Fourier transform of the
Coulomb potential by
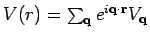 , where
, where
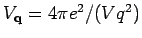 . Note that, since the Coulomb potential does not
have the periodicity of the lattice, wavevector
. Note that, since the Coulomb potential does not
have the periodicity of the lattice, wavevector 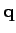 can take any value in
the reciprocal space and is not restricted within the first Brillouin zone.
Substituting in the above equation we get
can take any value in
the reciprocal space and is not restricted within the first Brillouin zone.
Substituting in the above equation we get
Since we are interested in finding the phonon frequencies for small values
of 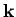 , it is tempting to take the limit
, it is tempting to take the limit
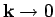 before
evaluating the sums. Such a procedure would show that the dynamical matrix
vanishes in this limit, implying that the phonon frequencies go to zero.
However, this would be incorrect. This is because the Coulomb potential is
long range, and so
before
evaluating the sums. Such a procedure would show that the dynamical matrix
vanishes in this limit, implying that the phonon frequencies go to zero.
However, this would be incorrect. This is because the Coulomb potential is
long range, and so 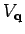 is singular for small values of
is singular for small values of 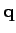 . We have
to be careful while dealing with singular functions, and the correct procedure
is to evaluate the sums and then take the limit
. We have
to be careful while dealing with singular functions, and the correct procedure
is to evaluate the sums and then take the limit
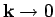 .
The integral over
.
The integral over
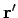 gives
gives
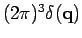 . The Dirac delta
function is converted into Kronecker delta by the replacement
. The Dirac delta
function is converted into Kronecker delta by the replacement
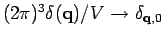 . This is the prescription for
going from continuous
. This is the prescription for
going from continuous 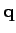 space to discrete
space to discrete 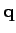 space. Since
space. Since 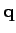 is not
restricted within the first Brillouin zone, we also get
is not
restricted within the first Brillouin zone, we also get
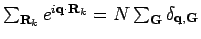 , where
, where 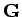 are reciprocal
lattice vectors. Using these in the above equation we get,
are reciprocal
lattice vectors. Using these in the above equation we get,
Having evaluated the dynamical matrix, we will now solve the eigenvalue
equation (5) for phonons of long wavelength (i.e.
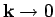 modes).
Suppose
modes).
Suppose
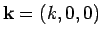 . Then, the dynamical matrix has the form,
. Then, the dynamical matrix has the form,
The non-diagonal elements of the matrix are zero due to the cubic symmetry of
the lattice. The longitudinal mode (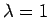 ), which is along the wavevector
), which is along the wavevector
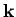 , should have eigenvector
, should have eigenvector
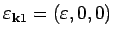 . Putting this
form
in equation (5) and noting that the dynamical matrix is diagonal, we get,
. Putting this
form
in equation (5) and noting that the dynamical matrix is diagonal, we get,
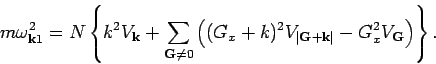 |
(8) |
In the limit
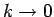 , only the first term on the right hand side
contribute, and we get
, only the first term on the right hand side
contribute, and we get
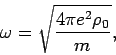 |
(9) |
which is the plasma frequency for the ions. If we keep the second term of
equation (8), we will get well behaved 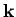 dependent corrections to
the plasma frequency for finite
dependent corrections to
the plasma frequency for finite 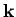 . It is important to note that
even in the long wavelength limit the longitudinal phonons have a finite
frequency. This is contrary to what we expect from Goldstone's theorem.
The breakdown of Goldstone's theorem is due to the long range nature of
the Coulomb potential. We can see that clearly from the first term of
equation (8) which gave us the finite plasma frequency. If the potential was
short range,
. It is important to note that
even in the long wavelength limit the longitudinal phonons have a finite
frequency. This is contrary to what we expect from Goldstone's theorem.
The breakdown of Goldstone's theorem is due to the long range nature of
the Coulomb potential. We can see that clearly from the first term of
equation (8) which gave us the finite plasma frequency. If the potential was
short range, 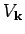 would be finite for vanishing
would be finite for vanishing 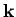 . Then, in the limit
. Then, in the limit
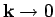 ,
,
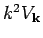 would vanish, and we would not have got
any finite frequency. It is also important to note that to see this effect it
is crucial to keep the contribution from the uniform background charge. The
background gives a
would vanish, and we would not have got
any finite frequency. It is also important to note that to see this effect it
is crucial to keep the contribution from the uniform background charge. The
background gives a 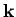 independent contribution to the longitudinal part of
independent contribution to the longitudinal part of
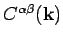 . Without this contribution, the spectrum of the longitudinal
phonons will reduce by a constant amount equal to the plasma frequency.
The two transverse modes have eigenvectors
. Without this contribution, the spectrum of the longitudinal
phonons will reduce by a constant amount equal to the plasma frequency.
The two transverse modes have eigenvectors
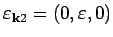 and
and
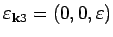 with eigenvalue equations
with eigenvalue equations
The two equations above are equivalent, and they give the same eigenvalue.
In the limit of
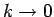 ,
,
Using equations (10) and (12), we find that the frequency of the long
wavelength transverse phonons is proportional to the wavevector, and is given
by
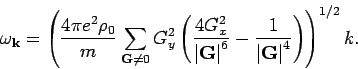 |
(13) |
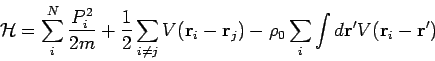
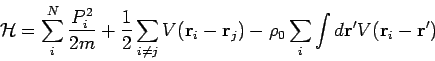
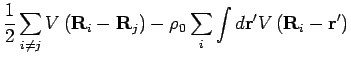
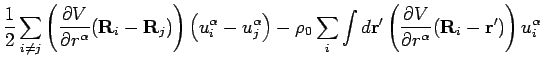
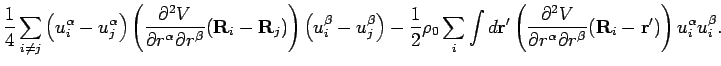
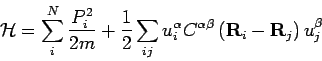
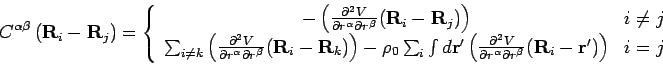
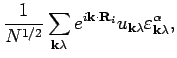
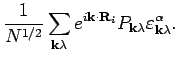
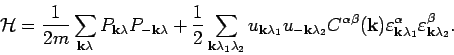
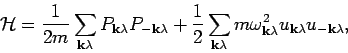
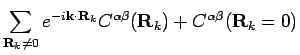
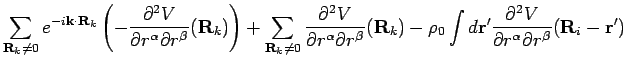
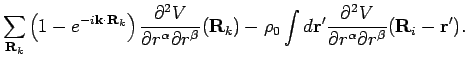
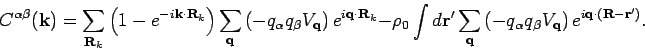
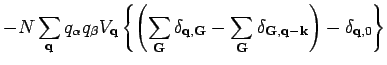
![$\displaystyle N \left[ k_{\alpha } k_{\beta } V_{{\bf k}} + \sum_{{\bf G}\neq 0...
... G}+ {\bf k}\right \vert}
- G_{\alpha }G_{\beta } V_{{\bf G}} \right\} \right].$](img56.gif)