We want to find the differential equation satisfied by the operator
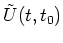 , which is defined as
, which is defined as
Here 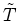 is the antichronological ordering operator defined as
is the antichronological ordering operator defined as
We examine the time evolution of
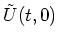 by comparing it with
by comparing it with
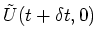 . We have,
. We have,
Here
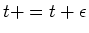 , with
, with
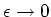 . Due to anti time ordering, in
the last line of the above expression,
. Due to anti time ordering, in
the last line of the above expression,
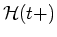 moves to the right of all
other terms. Thus,
moves to the right of all
other terms. Thus,
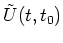 obeys the differential equation
obeys the differential equation
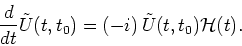 |
(2) |
![]() , which is defined as
, which is defined as
![\begin{displaymath}
\tilde{T}\left[ A(t_1) B(t_2) \right] = \left \{
\begin{arr...
..._1 < t_2) \\
B(t_2) A(t_1) & (t_1 > t_2).
\end{array} \right.
\end{displaymath}](img4.gif)
![]() by comparing it with
by comparing it with
![]() . We have,
. We have,
![$\displaystyle \tilde{T}{\rm exp} \left[ -i \int_{t_0}^{t} {\mathcal H}(\tau ) d \tau
-i \delta t {\mathcal H}(t+) \right]$](img9.gif)
![$\displaystyle \tilde{T}\sum_n \frac{(-i)^n}{n!} \left[ \int_{t_0}^{t} {\mathcal H}(\tau ) d \tau
+ \delta t {\mathcal H}(t+) \right]^n$](img10.gif)
![$\displaystyle \tilde{U}(t, t_0) + (-i) \tilde{T}\sum_{n=1}^{\infty} \frac{(-i)^...
...t_{t_0}^{t} {\mathcal H}(\tau ) d \tau \right]^{n-1}
+ {\mathcal O}(\delta t)^2$](img11.gif)