We want to examine the effect of hermitian conjugation on the operator expression
$T_{\gamma}{\rm exp} [ (-i) \int_{\gamma } {\mathcal H}(\tau ) d \tau ]$. The expression can be expanded as

$$T_{\gamma}{\rm exp} \left[ (-i) \int_{\gamma } {\mathcal H}(... ...t[ {\mathcal H}(\tau _1) \cdots {\mathcal H}(\tau _n) \right].$$ (1)

The time ordering operator $T_{\gamma}$ orders the operators along the directed path $\gamma$ such that, for example,

$$T_{\gamma}[ {\mathcal H}(z_2) {\mathcal H}(z_1) {\mathcal H}(z_N) ] = {\mathcal H}(z_N) {\mathcal H}(z_2) {\mathcal H}(z_1)$$

if $z_N > z_2 > z_1$ along the path $\gamma$.

We will first note the effect of hermitian conjugation on the integration measure of each term on the right hand side of equation (1). We get, $-i \rightarrow i$, $d \tau \rightarrow d \tau ^{\ast}$, and the limits of integration $(z_1, z_N) \rightarrow (z_1^{\ast}, z_N^{\ast})$. The difference of a negative sign can be absorbed by reversing the limits of integration. Thus

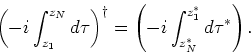$$\left( -i \int_{z_1}^{z_N} d \tau \right)^{\dagger} = \left( -i \int_{z_N^{\ast}}^{z_1^{\ast}} d \tau ^{\ast} \right).$$ (2)

Next, we will examine the behaviour of the integrand, which is a product of time ordered operators, under hermitian conjugation. Let us look at $T_{\gamma}[ {\mathcal H}(\tau _1) {\mathcal H}(\tau _2) \cdots {\mathcal H}(\tau _m) ]$ where, for definiteness, we assume $\tau _1 < \tau _2 < \cdots < \tau _m$ as we go along some path $\gamma$. Then,

$$\left[T_{\gamma}\left( {\mathcal H}(\tau _1) {\mathcal H}(\tau _2) \cdots {\mathcal H}(\tau _m) \right)\right] ^{\dagger} = \left[ {\mathcal H}(\tau _m) \cdots {\mathcal H}(\tau _2) {\mathcal H}(\tau _1) \right]^{\dagger}$$

$$= {\mathcal H}(\tau _1)^{\dagger} {\mathcal H}(\tau _2)^{\dagger} \cdots {\mathcal H}(\tau _m)^{\dagger}$$

$$= \tilde{{\mathcal H}}(\tau _1^{\ast})\tilde{{\mathcal H}}(\tau _2^{\ast}) \cdots \tilde{{\mathcal H}}(\tau _m^{\ast})$$

$$= T_{\tilde{\gamma}}\left[ \tilde{{\mathcal H}}(\tau _1^{\ast})\til... ...athcal H}}(\tau _2^{\ast}) \cdots \tilde{{\mathcal H}}(\tau _m^{\ast}) \right].$$ (3)

In the last but one line of the above equation we have used the definition $\tilde{{\mathcal H}}(z) = ({\mathcal H}(z^{\ast}))^{\dagger}$. From the expression in this line we see that the effect of hermitian conjugation on a product of operators time ordered along the contour $\gamma = (z_1, z_N)$, is to time order the operators along the contour $\tilde{\gamma}= (z_N^{\ast}, z_1^{\ast})$.

From equations (1), (2) and (3) we can therefore write,

$$\left(T_{\gamma}{\rm exp} \left[ (-i) \int_{\gamma } {\mathcal H}(\tau ) d \tau \right]\right) ^{\dagger} = \sum_n \frac{(-i)^n}{n!} \int_{z_N^{\ast}}^{z_1^{\ast}} d \tau _1... ...\left[ {\mathcal H}(\tau _1^{\ast}) \cdots {\mathcal H}(\tau _n^{\ast}) \right]$$

$$= \left(T_{\tilde{\gamma}}{\rm exp} \left[ (-i) \int_{\tilde{\gamma}} \tilde{{\mathcal H}}(\tau ) d \tau \right]\right) ^{\dagger}.$$ (4)