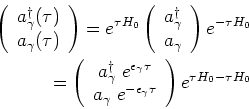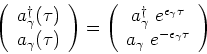a. I use 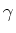 instead of what's on the homework assignment so that I can keep the labels straight.
instead of what's on the homework assignment so that I can keep the labels straight. 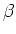 has a negative sign so that the partition function is bounded.
has a negative sign so that the partition function is bounded.
where
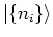 stands for a many particle state with
a set,
stands for a many particle state with
a set, 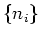 , of occupation numbers.
, of occupation numbers.
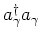 acting on
acting on
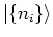 returns 0 or 1
depending on whether there is a fermion in state
returns 0 or 1
depending on whether there is a fermion in state 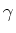 -
Alas, the notation is a bit degenerate -
We can likewise get the eigenvalues for the operators in the H-potential. I will use
-
Alas, the notation is a bit degenerate -
We can likewise get the eigenvalues for the operators in the H-potential. I will use
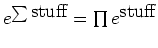 , and write
, and write
Now, I let the density operators act on the various 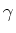 states.
states.
Take the term which was generated by the state 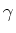 out of the product.
out of the product.
Do the sum over occupation numbers 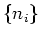 with
with 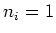 or
or 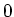 .
.
b.
Solve
using
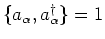 . We know the first term on the left from part a.
The second term doesn't take too much effort to get.
. We know the first term on the left from part a.
The second term doesn't take too much effort to get.
So
Which can be rewritten
c.
Noting that
We can find
>From earlier,
whence it follows
which is what I got in part a.
d.
and
so
e.
For bosons,
First, we get the partition function. Notice that all for each 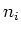 , all positive integer values are allowed. The sum is a geometric series and can be done explicitly.
, all positive integer values are allowed. The sum is a geometric series and can be done explicitly.
Then, we use a nice little trick.
When one of the energies is zero or
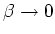 , the bose function diverges, and we get a condensate.
, the bose function diverges, and we get a condensate.
Finally, I need to find
![$\mbox{Trace}\left[e^{-\beta H_0} a_\gamma a_\gamma^\dagger \right]$](img31.gif) . Use the commutator to shuffle terms.
. Use the commutator to shuffle terms.
f.
We work with bosons.
So
![$[H_0,a_\gamma]=-\epsilon_\gamma a_\gamma$](img35.gif) and
and
![$[H_0,a^\dagger_\gamma]=\epsilon_\gamma a^\dagger_\gamma$](img36.gif) .
.
So commuting the 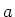 and
and 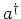 s past the
s past the 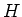 , we find
, we find
![\begin{eqnarray*}
\mbox{Trace}\left[e^{-\beta H_0} a_\gamma^\dagger a_\gamma \ri...
...beta H_0}
a_\gamma^\dagger a_\gamma \right] \vert\{n_i\}\rangle
\end{eqnarray*}](img4.gif)
![\begin{eqnarray*}
\mbox{Trace}\left[e^{-\beta H_0} a_\gamma^\dagger a_\gamma \ri...
...beta H_0}
a_\gamma^\dagger a_\gamma \right] \vert\{n_i\}\rangle
\end{eqnarray*}](img4.gif)
![\begin{eqnarray*}
\mbox{Trace}\left[e^{-\beta H_0} a_\gamma^\dagger a_\gamma \ri...
...a
\prod_\alpha \left[e^{-\beta \epsilon_\alpha n_\alpha} \right]
\end{eqnarray*}](img9.gif)
![\begin{eqnarray*}
\mbox{Trace}\left[e^{-\beta H_0} a_\gamma^\dagger a_\gamma \ri...
...a\neq\gamma} \left[e^{-\beta \epsilon_\alpha n_{\alpha}} \right]
\end{eqnarray*}](img10.gif)
![\begin{eqnarray*}
\mbox{Trace}\left[e^{-\beta H_0} a_\gamma^\dagger a_\gamma \ri...
...d_{\alpha\neq\gamma} \left[ 1+e^{-\beta \epsilon_\alpha} \right]
\end{eqnarray*}](img13.gif)
![\begin{eqnarray*}
\mbox{Trace}\left[e^{-\beta H_0} \right] = \sum_{\{n_i\}} \pro...
...\rangle
= \prod_\alpha \left(1+e^{-\beta \epsilon_\alpha}\right)
\end{eqnarray*}](img16.gif)
![\begin{eqnarray*}
\mbox{Trace}\left[e^{-\beta H_0} a_\gamma a_\gamma^\dagger \ri...
...}}\right]
\prod_\alpha \left(1+e^{-\beta \epsilon_\alpha}\right)
\end{eqnarray*}](img17.gif)
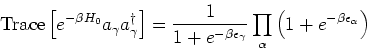
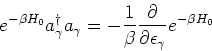
![\begin{eqnarray*}
\mbox{Trace}\left[e^{-\beta H_0} a_\gamma^\dagger a_\gamma \ri...
...partial \epsilon_\gamma}
\mbox{Trace}\left[e^{-\beta H_0}\right]
\end{eqnarray*}](img20.gif)
![\begin{eqnarray*}
\mbox{Trace}\left[e^{-\beta H_0} a_\gamma^\dagger a_\gamma \ri...
...d_{\alpha\neq\gamma} \left[ 1+e^{-\beta \epsilon_\alpha} \right]
\end{eqnarray*}](img13.gif)
![\begin{eqnarray*}
\mbox{Trace}\left[e^{-\beta H_0} a_\gamma^\dagger a_\gamma \ri...
...mma} }
\prod_{\alpha} \left[1+e^{-\beta \epsilon_\alpha }\right]
\end{eqnarray*}](img23.gif)
![\begin{eqnarray*}
\langle n_\gamma \rangle =
\mbox{Trace}\left[e^{-\beta H_0} a_...
...e^{-\beta H_0}\right] \\
= \frac{1}{1+e^{\beta\epsilon_\gamma}}
\end{eqnarray*}](img24.gif)
![\begin{eqnarray*}
\mbox{Trace}\left[ e^{-\beta H_0}\right] = Z
= \sum_{\{n_i\}} ...
...ha}}\\
= \prod_{\alpha} \frac{1}{1-e^{-\beta \epsilon_\alpha} }
\end{eqnarray*}](img27.gif)
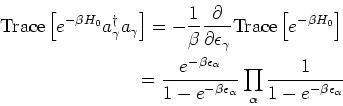
![\begin{eqnarray*}
\langle n_\gamma \rangle = \mbox{Trace}\left[e^{-\beta H_0} a_...
...{-\beta H_0} \right]\\
=
\frac{-1}{1-e^{\beta \epsilon_\gamma}}
\end{eqnarray*}](img29.gif)
![]() . Use the commutator to shuffle terms.
. Use the commutator to shuffle terms.
![\begin{eqnarray*}[a_\gamma, H_0]=
\sum_\alpha \epsilon_\alpha [a_\gamma, a^\dagg...
...\gamma,a_\gamma a^\dagger_\gamma] \\
= \epsilon_\gamma a_\gamma
\end{eqnarray*}](img33.gif)
![\begin{eqnarray*}[a^\dagger_\gamma, H_0]=
\sum_\alpha \epsilon_\alpha [a^\dagger...
...\dagger_\gamma a_\gamma] \\
= -\epsilon_\gamma a^\dagger_\gamma
\end{eqnarray*}](img34.gif)