For the spin ![]() fermions we want to prove the ``Hubbard Stratonovich''
operator identity
fermions we want to prove the ``Hubbard Stratonovich''
operator identity
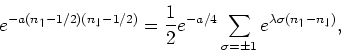 |
(1) |
In this basis we will represent the states
by
![]() , i.e.,
, i.e., ![]() is the empty state,
is the empty state, ![]() is
the single spin-up state,
is
the single spin-up state, ![]() is the single spin-down state, and
is the single spin-down state, and
![]() is the doubly occupied state. For brevity, we will call
is the doubly occupied state. For brevity, we will call
![]() , and
, and
![]() .
.
We find that,
![]() , and
, and
![]() . Similarly, we
have,
. Similarly, we
have,
![]() .
.
Next, we find that
![]() ,
and
,
and
![]() .
And, similarly,
.
And, similarly,
![]() . Thus, in general,
. Thus, in general,
| (2) |