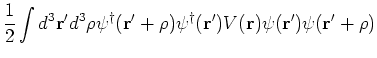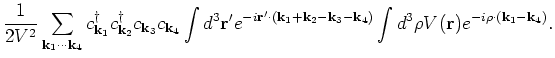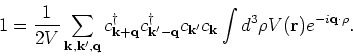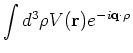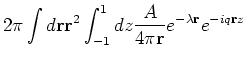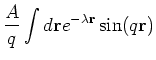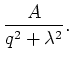We want to write the Hamiltonian in the second quantized notation for a system
of fermions interacting under the Yukawa potential. First we deal with the
kinetic energy term which is a one body operator. In the formalism of second
quantization this is written as
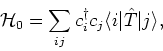 |
(1) |
where
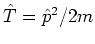 , the states
, the states 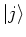 define an arbitrary
basis of the single particle Hilbert space, and
define an arbitrary
basis of the single particle Hilbert space, and 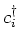 and
and 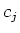 are
fermionic operators obeying anticommutation relation
are
fermionic operators obeying anticommutation relation
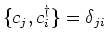 . To represent
. To represent
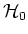 in the position basis we use the completeness
condition for the single particle Hilbert space, namely
in the position basis we use the completeness
condition for the single particle Hilbert space, namely
We get,
Now,
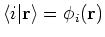 is the representation of the state
is the representation of the state
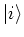 in the position basis (wavefunction). We also note that
in the position basis (wavefunction). We also note that
Then,
We define the creation field operator as
and similarly the annihilation operator
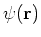 . Then we can write
. Then we can write
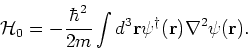 |
(2) |
The two body interaction term is written as
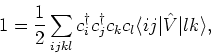 |
(3) |
where
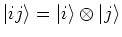 is a state of the two particle
Hilbert space. Using the completeness condition
is a state of the two particle
Hilbert space. Using the completeness condition
for the two particle Hilbert space, we get
We will now rewrite the Hamiltonian in the momentum basis. For this we define
the Fourier transform of the field operators as
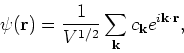 |
(5) |
and similarly for
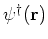 . Here
. Here 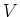 is the volume of the system. Using
this definition in equation (2) we get,
is the volume of the system. Using
this definition in equation (2) we get,
In the above equation we have used the definition of Kronecker delta
To write the interaction term in the momentum basis we first introduce a
new variable
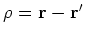 . From equation (4) we get
. From equation (4) we get
Now,
which gives overall momentum conservation for the two particle scattering
process. We write
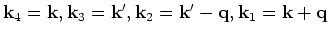 . Then we get,
. Then we get,
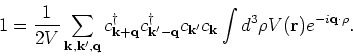 |
(7) |
The Yukawa potential is given by
Its Fourier transform is given by
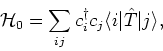
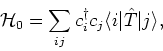

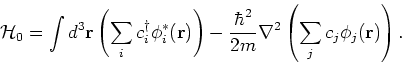
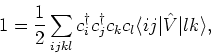
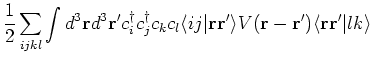
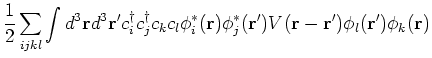
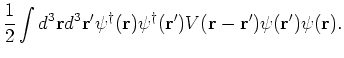
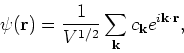
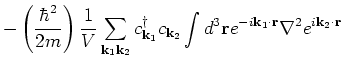
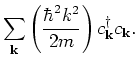
![]() . From equation (4) we get
. From equation (4) we get