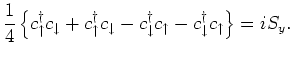We want to show that the Heisenberg spin operator 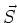$\vec{S}$ (spin-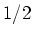$1/2$ objects) can be expressed in terms fermionic operators as

$\displaystyle S_x$ $\textstyle =$ $\displaystyle \frac{1}{2} \left( c^{\dagger}_{\uparrow}c_{\downarrow}+ c^{\dagger}_{\downarrow}c_{\uparrow}\right),$  
$\displaystyle S_y$ $\textstyle =$ $\displaystyle - \frac{i}{2} \left( c^{\dagger}_{\uparrow}c_{\downarrow}- c^{\dagger}_{\downarrow}c_{\uparrow}\right),$  
$\displaystyle S_z$ $\textstyle =$ $\displaystyle \frac{1}{2} \left( c^{\dagger}_{\uparrow}c_{\uparrow}- c^{\dagger}_{\downarrow}c_{\downarrow}\right).$  

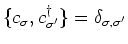It is enough to verify that the above representation of the spin operators satisfy the correct commutation relations. We will use the anticommutation property of the fermionic operators, namely $\{ c_{\sigma } , c^{\dagger}_{\sigma^{\prime}} \} = \delta_{\sigma , \sigma^{\prime}}$.

Thus, we have

$\displaystyle \left[ S_x , S_y \right]$ $\textstyle =$ $\displaystyle - \frac{i}{4} \left[ c^{\dagger}_{\uparrow}c_{\downarrow}+ c^{\da... ...{\dagger}_{\uparrow}c_{\downarrow}- c^{\dagger}_{\downarrow}c_{\uparrow}\right]$  
  $\textstyle =$ $\displaystyle - \frac{i}{2} \left[ c^{\dagger}_{\downarrow}c_{\uparrow}, c^{\dagger}_{\uparrow}c_{\downarrow}\right]$  
  $\textstyle =$ $\displaystyle - \frac{i}{2} \left( c^{\dagger}_{\downarrow}c_{\downarrow}- c^{\dagger}_{\uparrow}c_{\uparrow}\right) = i S_z.$ (1)

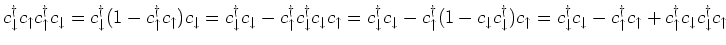To evaluate the commutator in the last but one line in the above equation, we have used $c^{\dagger}_{\downarrow}c_{\uparrow}c^{\dagger}_{\uparrow}c_{\downarrow}= c^{\d... ...rrow}+ c^{\dagger}_{\uparrow}c_{\downarrow}c^{\dagger}_{\downarrow}c_{\uparrow}$ .

Next, we have,

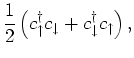
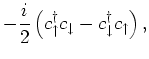
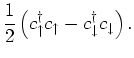
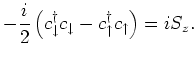
$\displaystyle \left[ S_y , S_z \right]$ $\textstyle =$ $\displaystyle - \frac{i}{4} \left\{ \left[ c^{\dagger}_{\uparrow}c_{\downarrow}... ...\downarrow}c_{\uparrow}, c^{\dagger}_{\downarrow}c_{\downarrow}\right] \right\}$  
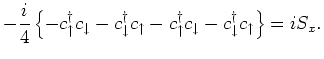
  $\textstyle =$ $\displaystyle - \frac{i}{4} \left\{ - c^{\dagger}_{\uparrow}c_{\downarrow}- c^{... ...\uparrow}c_{\downarrow}- c^{\dagger}_{\downarrow}c_{\uparrow} \right\} = i S_x.$ (2)

Finally, we have,

$\displaystyle \left[ S_z , S_x \right]$ $\textstyle =$ $\displaystyle \frac{1}{4} \left\{ \left[ c^{\dagger}_{\uparrow}c_{\uparrow}, c^... ...\downarrow}c_{\downarrow}, c^{\dagger}_{\downarrow}c_{\uparrow}\right] \right\}$  
  $\textstyle =$ $\displaystyle \frac{1}{4} \left\{ c^{\dagger}_{\uparrow}c_{\downarrow}+ c^{\dag... ...{\downarrow}c_{\uparrow}- c^{\dagger}_{\downarrow}c_{\uparrow}\right\} = i S_y.$ (3)