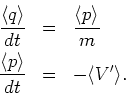In the following problems, a unit system so that 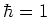 and
and 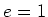 is used.
is used.
a. The equation of motion is
Substitute
into
to get
using
![$[\hat{x}_j,\hat{p}_k]=i\delta_{jk}$](img8.gif) . This shows that that
. This shows that that 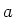 and
and 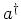 can be considered as an operator factorization of H. Note that these so called creation and annihilation operators satisfy the following commutation relationship,
can be considered as an operator factorization of H. Note that these so called creation and annihilation operators satisfy the following commutation relationship,
Write out the commutator explicitly and commute the 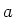 and
and 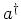 in the first term.
in the first term.
Upon integration
b.
Given
And from part a
so
Add these
Solve for 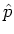
To get 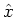 , subtract
, subtract
Solve for 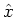
c. We know that
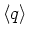 and
and
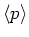 obey the Erenfest
theorem and we can write:
obey the Erenfest
theorem and we can write:
And they are equivalent to classical equations when
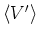 =
=
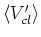 . If dispersion
. If dispersion
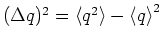 of wave packet is small then we can write:
of wave packet is small then we can write:
We see that 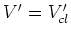 if all term higher that
if all term higher that 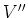 are equal
to zero. Harmonic oscillator potential has quadratic form and
hence quantum and classical equation of motion look similar.
are equal
to zero. Harmonic oscillator potential has quadratic form and
hence quantum and classical equation of motion look similar.
![\begin{eqnarray*}
a = \frac{1}{\sqrt{2}}
\left[\frac{1}{\sqrt{m\omega}} \hat{p}- i \sqrt{m\omega} \hat{x}\right]
\end{eqnarray*}](img4.gif)
![\begin{eqnarray*}
a^\dagger = \frac{1}{\sqrt{2}}
\left[\frac{1}{\sqrt{m\omega}} \hat{p}+ i \sqrt{m\omega} \hat{x}\right]
\end{eqnarray*}](img5.gif)
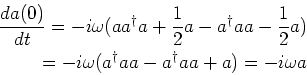
![\begin{eqnarray*}
a^\dagger (0) = \frac{1}{\sqrt{2}}
\left[\frac{1}{\sqrt{m\omega}} \hat{p}(0) + i \sqrt{m\omega} \hat{x}(0) \right]
\end{eqnarray*}](img15.gif)
![\begin{eqnarray*}
a(t) = \frac{1}{\sqrt{2}}
\left[\frac{1}{\sqrt{m\omega}} \hat{...
...ga}} \hat{p}(t) - i \sqrt{\frac{1}{2}m\omega} \hat{x}(t) \right]
\end{eqnarray*}](img16.gif)
![\begin{eqnarray*}
a^\dagger(t) = \frac{1}{\sqrt{2}}
\left[\frac{1}{\sqrt{m\omega...
...ga}} \hat{p}(t) + i \sqrt{\frac{1}{2}m\omega} \hat{x}(t) \right]
\end{eqnarray*}](img17.gif)
![\begin{eqnarray*}
a(t)+a^\dagger(t)=
\sqrt{\frac{2}{m\omega}} \hat{p}(t)
=
\frac...
...\omega}{2}} \hat{x}(0) \left[e^{i\omega t}-e^{-i\omega t}\right]
\end{eqnarray*}](img18.gif)
![\begin{eqnarray*}
a^\dagger(t)-a(t)=
\sqrt{2 m\omega} \hat{x}(t)
=
\frac{1}{\sqr...
...\omega}{2}} \hat{x}(0) \left[e^{i\omega t}+e^{-i\omega t}\right]
\end{eqnarray*}](img22.gif)
![]() and
and
![]() obey the Erenfest
theorem and we can write:
obey the Erenfest
theorem and we can write: