| (1) |
Exercise N5
The a.c. conductivity of a system of interacting electron is given by
where
![]() is the retarded current-current correlation
function
is the retarded current-current correlation
function
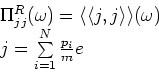
Prove the ![]() -sum rule:
-sum rule:
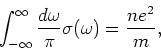
Hints:
Express (1) in terms of the spectral function of the current
![]() which is odd.
which is odd.
Relate
![]() to
to
![]() , where
, where ![]() is operator such that
is operator such that
![]() . Apply the sum rule for
. Apply the sum rule for
![]() that we learned in class.
that we learned in class.