


Next: The Interaction Strength and
Up: Toward a Symmetrization of
Previous: Introduction
To postulate a force that varies as
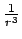 suggests that it
operates in four spatial dimensions. In a universe devoid of any clustering
of ordinary matter, such a repelling system would be modelled as a uniform, continuous fluid, obeying Birkhoff's theorem for four dimensions. When the ordinary matter, M, begins to cluster, it attracts the
suggests that it
operates in four spatial dimensions. In a universe devoid of any clustering
of ordinary matter, such a repelling system would be modelled as a uniform, continuous fluid, obeying Birkhoff's theorem for four dimensions. When the ordinary matter, M, begins to cluster, it attracts the
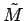 . If the
. If the
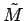 is compressible,
we can easily envision an equilibrium configuration whereby gravity is
completely neutralized by density gradients set up by the
is compressible,
we can easily envision an equilibrium configuration whereby gravity is
completely neutralized by density gradients set up by the
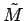 . However, if the
. However, if the
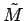 fluid has a maximum allowable density (or is incompressible), it can now yield localized regions that can augment the gravitational field due to the M alaone. For example, it is possible for a localized region of self-repelling
fluid has a maximum allowable density (or is incompressible), it can now yield localized regions that can augment the gravitational field due to the M alaone. For example, it is possible for a localized region of self-repelling
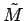 to form a shell surrounding the real M, attracted toward the center of the potential well by the Newtonian field, and repelled by the bulk of the
to form a shell surrounding the real M, attracted toward the center of the potential well by the Newtonian field, and repelled by the bulk of the
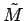 in the shell.
The problem with this picture is that it is difficult to see how, in a 4-dimensional manifold, one can have an inverse cube law for one interaction, and an inverse square law for another. We point out the recent finding by Randall and Sundrum (2000), which claims that the standard experimental results for gravity (such as obedience to a 3 dimensional Poisson equation) is consistent with even an infinite 4th spatial dimension, if the component of the metric in the new dimension depends on the coordinates in that dimension.
Moreover, Dvali, Gabadadze and Porrati (2000) have shown that even in a infinite flat 4D space, at large distances there can be a natural scaling of the potential as
in the shell.
The problem with this picture is that it is difficult to see how, in a 4-dimensional manifold, one can have an inverse cube law for one interaction, and an inverse square law for another. We point out the recent finding by Randall and Sundrum (2000), which claims that the standard experimental results for gravity (such as obedience to a 3 dimensional Poisson equation) is consistent with even an infinite 4th spatial dimension, if the component of the metric in the new dimension depends on the coordinates in that dimension.
Moreover, Dvali, Gabadadze and Porrati (2000) have shown that even in a infinite flat 4D space, at large distances there can be a natural scaling of the potential as
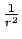 while preserving Newtonian gravity at small distances.
Without going into more detail here, we merely accept this as a possibility and explore the phenomenological consequences of our postulated interaction.
while preserving Newtonian gravity at small distances.
Without going into more detail here, we merely accept this as a possibility and explore the phenomenological consequences of our postulated interaction.
Returning to the simple configuration of a shell of
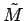 material as outlined above, we can evaluate the potential at any point P in the shelll's interior:
material as outlined above, we can evaluate the potential at any point P in the shelll's interior:
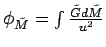 , where
, where 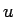 is the distance from a point on the shell with mass element
is the distance from a point on the shell with mass element
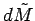 to to the point P. The
integration is straightforward and we find:
to to the point P. The
integration is straightforward and we find:
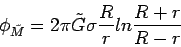 |
(3) |
where R is the radius of the
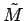 shell,
shell, 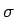 is its surface density on the 3-sphere, and r is the radial displacement of P from the center of the shell. We immediately
find the field:
is its surface density on the 3-sphere, and r is the radial displacement of P from the center of the shell. We immediately
find the field:
![\begin{displaymath}
\vert\tilde{g}(r)\vert = \frac{ 2 \pi \tilde{G}\sigma R}{r} ...
...c{1}{r} ln \frac{R+r}
{R-r} - \frac{2R}{R^{2} - r^{2}} \right]
\end{displaymath}](img21.gif) |
(4) |
directed radially inward.
For r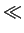 R, expanding the logarithm yields the following result for the
acceleration:
R, expanding the logarithm yields the following result for the
acceleration:
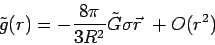 |
(5) |
The
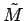 on the surface of the sphere thus pushes inward differentially near M, effectively augmenting the gravitational potential due to the real mass alone. Of course, the configuration surrounding a flattened system will be
different, but the above should be sufficient to demonstrate that this idea holds the possibility of solving the dark matter problem. For a required velocity of
on the surface of the sphere thus pushes inward differentially near M, effectively augmenting the gravitational potential due to the real mass alone. Of course, the configuration surrounding a flattened system will be
different, but the above should be sufficient to demonstrate that this idea holds the possibility of solving the dark matter problem. For a required velocity of
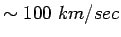 at r=10 kpc, for example, we could have R=30 kpc with a total
at r=10 kpc, for example, we could have R=30 kpc with a total
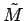
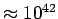 gm in the shell. It is clear that the
gm in the shell. It is clear that the
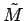 will not be confined to a shell, and ought to fill space between the galaxies, but the dominant portion of interaction will be from the regions closest to the galactic center, since the
will not be confined to a shell, and ought to fill space between the galaxies, but the dominant portion of interaction will be from the regions closest to the galactic center, since the 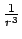 interaction will fall off rapidly as R gets larger.
Moreover, as r
interaction will fall off rapidly as R gets larger.
Moreover, as r
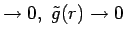 , thus recovering a purely Newtonian field.
, thus recovering a purely Newtonian field.



Next: The Interaction Strength and
Up: Toward a Symmetrization of
Previous: Introduction
Terry Matilsky
![]() material as outlined above, we can evaluate the potential at any point P in the shelll's interior:
material as outlined above, we can evaluate the potential at any point P in the shelll's interior:
![]() , where
, where ![]() is the distance from a point on the shell with mass element
is the distance from a point on the shell with mass element
![]() to to the point P. The
integration is straightforward and we find:
to to the point P. The
integration is straightforward and we find:
![\begin{displaymath}
\vert\tilde{g}(r)\vert = \frac{ 2 \pi \tilde{G}\sigma R}{r} ...
...c{1}{r} ln \frac{R+r}
{R-r} - \frac{2R}{R^{2} - r^{2}} \right]
\end{displaymath}](img21.gif)
![]() R, expanding the logarithm yields the following result for the
acceleration:
R, expanding the logarithm yields the following result for the
acceleration:
![]() on the surface of the sphere thus pushes inward differentially near M, effectively augmenting the gravitational potential due to the real mass alone. Of course, the configuration surrounding a flattened system will be
different, but the above should be sufficient to demonstrate that this idea holds the possibility of solving the dark matter problem. For a required velocity of
on the surface of the sphere thus pushes inward differentially near M, effectively augmenting the gravitational potential due to the real mass alone. Of course, the configuration surrounding a flattened system will be
different, but the above should be sufficient to demonstrate that this idea holds the possibility of solving the dark matter problem. For a required velocity of
![]() at r=10 kpc, for example, we could have R=30 kpc with a total
at r=10 kpc, for example, we could have R=30 kpc with a total
![]()
![]() gm in the shell. It is clear that the
gm in the shell. It is clear that the
![]() will not be confined to a shell, and ought to fill space between the galaxies, but the dominant portion of interaction will be from the regions closest to the galactic center, since the
will not be confined to a shell, and ought to fill space between the galaxies, but the dominant portion of interaction will be from the regions closest to the galactic center, since the ![]() interaction will fall off rapidly as R gets larger.
Moreover, as r
interaction will fall off rapidly as R gets larger.
Moreover, as r
![]() , thus recovering a purely Newtonian field.
, thus recovering a purely Newtonian field.