On the bottom of the page there are two rows of six links within HEASARC to which you can go. The top left option is the W3Browse location where you can search for observations of various objects.
- Click on it.
- Select the Basic option.
- From the Active Mission Archives section select ROSAT by clicking on the gray button to its left.
- In the box at the top labeled Object Name or Coordinates enter GK PER.
- Click on Submit Query.
- Select the second observation whose instrument is the PSPCB.
- Slightly below the table of observations there is a box, entitled
Categories of data products, containing different types of data
collected in each observation. Click on the gray Submit button below.
You may receive a security warning message from Netscape, to continue
just click on Continue Submission.
- This page shows all the possible data that can be examined from the observation you chose. At the end of each line the filename of the data you wish to retrieve is printed in the form of file.Z. Select the Basic Science Events file by clicking on the gray button on its left.
- Scroll down the page and click on Retrieve Data Products
- The screen that appears should list the file you chose. Click on
Download TAR file which appears right below.
- The window that appears contains four sections: Filter,
Directories, Files, Selection. Make sure that your directory apears
in the Selection box. If it does not then you must enter the
/temp directory you created to store your files.
If you had to re-enter your directory then when you finished typing click on Cancel, then Click on Download TAR file again. This time the correct directory should appear in the Selection box.
- Click on OK
Netscape will copy the files you have selected into your directory in the form of a w3browse-
 .tar file. It is a compressed file
and cannot be used until it is opened up properly.
.tar file. It is a compressed file
and cannot be used until it is opened up properly.
- Un-tar your w3browse-
 .tar by typing:
.tar by typing:
tar -vxf w3browse-
 .tar < Enter >
.tar < Enter >
This command produced a subdirectory chain in your directory called rp300217n00/ where youre files are located.
- You will find the files you downloaded from HEASARC in their new
subdirectory by typing:
cd rp300217n00/
- File completion.
If the name of the file (or directory) you are entering reaches a unique string (for example if you had entered rp3 above and there were no other files in your directory with this beginning) you may press the
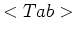 key and the filename will be completed.
If the string is not unique then the name will complete up to the
point where it becomes ambiguous and you must add a character to make
it unique - then you can press
key and the filename will be completed.
If the string is not unique then the name will complete up to the
point where it becomes ambiguous and you must add a character to make
it unique - then you can press  to complete it again.
to complete it again.
- Then type ls < Enter > to list the files.
rp300217n00_bas.fits.Z should appear.
Notice the file ends with .Z
 . This means it is comrpessed
further and still cannot be used.
. This means it is comrpessed
further and still cannot be used.
- Uncompress the files by typing:
uncompress *.Z < Enter >
The * is a wildcard character so that your command above says ``uncompress anything in this directory that ends with .Z''.
Then type ls < Enter > . The .Z should have disappeared from the filename making the file usable.
- Remove the w3browse-
 .tar file now that you have what you
need by returning to the directory to which you downloaded it and
typing:
.tar file now that you have what you
need by returning to the directory to which you downloaded it and
typing:
rm w3browse-
 .tar < Enter > or
.tar < Enter > or
rm w3 < Tab > < Enter > and allow the file completion feature to do its work.
emacs rp300217n00_bas.fits ![]() < Enter >
< Enter >
The file that comes up contains information such as the date and time of this observation, the telescope and instrument that collected the data, the location of the object as well as its name.
Close emacs.
- The program you are using to process and analyze the data from
HEASARC, ftools contains a package (i.e. subprogram) named Xselect which contains all the commands you will need to look at the
images from your data, and examine lightcurves and power spectra.
- To use Xselect you must execute its commands. At the prompt
type:
Xselect < Enter >
- You will be asked to enter a session (so that when you are done you
can save all your work into that session or continue where you left
off).
Call your session session1 < Enter >.
- Notice the information that appears on the screen is specific for ASCA - a different satellite. We want to analyze ROSAT data and
we need to tell Xselect to do so. Type:
read events < Enter >
- You will be asked in which directory do the event files exist. If you
called up Xselect from the directory where youre ROSAT files
exist then enter ./ < Enter > (which means this directory).
- Then enter the name of your file: rp300217n00_bas.fits < Enter
> or, again, you may type rp < Tab > < Enter >.
- Type yes < Enter > to reset the mission.
Now Xselect is configured. Notice the important notes that follow on your screen.
Notes: XSELECT set up for ROSAT
Keywords for time and pha are TIME PI
Units of time are s
Default timing binsize= 16.000This data and that which follows describes how the program is now configured to handle your data. For example, it tells that the units of time in any process will be in seconds. It also prints the directory where your data is located. Finally, the program outputs the information about your object, GK PER, its position in the sky, the livetime (how long the detector was taking data on this object), and the date of observation.
Xselect has some general commands that you will be using to create images, light curves, and energy spectra. Here are some of the commands (and their descriptions) that you will be using the most.
- Read events, which you have already used in the previous
section, enters data into the program. If you wish to enter a new set
of data, you can do it with this command
- Filter commands do no work. They merely enter filters selecting
a particular region or time interval that will be applied to the next
run of the extract command.
- Extract command produces a product file such as an image, a
spectrum, or a lightcurve.
- Clear command is used to clear any changes you have made to
data and restores it to the way it was originally.
- Another useful command is show data which you can type at any
time and you will receive an output of your working directory and the
names of the files you are using.
- Similar to the ls command, to list all the files in your current
directory you can type list workdirectory or list
datadirectory.
- The
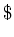 symbol allows you to exit Xselect temporarily without
quitting so that you may move around your directory tree, copy or
delete files, and then return to Xselect where you left off by
typing exit.
symbol allows you to exit Xselect temporarily without
quitting so that you may move around your directory tree, copy or
delete files, and then return to Xselect where you left off by
typing exit.
- To look at GK PER you need to command Xselect to show it
to you. At the prompt type:
extract image < Enter >
Once again Xselect prints out information on the screen. The important facts are the seconds and the counts that provide a countrate for the image. This is important because a high countrate means the object was giving off photons at a high rate and will be bright. A very low countrate implies a faint or no image (just noise).
- The image has been extracted from the data and you must now use an
imaging tool to look at it. Type saoimage < Enter > to call up the
imaging tool. A new window should pop up with your data displayed
upon it.
SAOIMAGE
You should take some time to familiarize yourself with this tool. You can change the features of your display by selecting a ``button'' from the top row. If you click on Scale, for example, you have a choice, on the seconds row, of viewing your image in a variety of brightness scales. Notice the grayscale legend at the bottom. A linear scaling would let the brightest thing in your image be the color of the extreme right, the least bright thing in your image be the color of the extreme left, and the values in between would be evenly spaced along the grayscale legend. A square root display would let the square root of the maximum and minimum brightness values be displayed as the leftmost and rightmost grayscale values. Try the logarithmic scaling to see what it does.
You can also change the color schemes by clicking on Color. The button cmap will add more choices to your display options. You can invert the grayscale legend by clicking on invert. To return to the color options click on cmap again.
You can mark your object of choice with a cursor and define a region to later observe.
- The object we are examining is GK PER. It is located at the bottom
left of the display.
If you want to center your object click on Pan and then click on
the object. It should move to the center. Then click on Cursor.
- Select a circle shaped cursor. With your mouse button choose a circle
size that places your object comfortably inside. The left mouse
button puts the center of your shape in place, and clicking down on
both mouse buttons allows you to drag out the radius of the shape to
any size you wish. Make your circle just big enough to enclose the
star. Then type s on the keyboard to ``save'' the region.
- Click on the button labeled region (the rest of the buttons
should change) and select write. On the line that appears type
a unique filename for your region which saves the region surrounding
your object for later use.
Continue to play with SAOimage until you feel comfotable using it.
- The object we are examining is GK PER. It is located at the bottom
left of the display.
If you want to center your object click on Pan and then click on
the object. It should move to the center. Then click on Cursor.
- To look at the data inside your selected region only, return to the
window where Xselect is running and type:
filter region src.reg < Enter >
When you apply the filter command to an image it is as if you are placing an opaque screen with a hole in it over the data. The hole in the screen is the region you selected.
- Next you must type extract events < Enter > to select only the data
contained in your region. In other words, you are choosing only the
points that show through the hole in the screen. The rest are
ignored. The output of this command should show a Grand Total
of 112910 counts with a much smaller number (around 3 or 4 thousand)
of Good counts and the rest are Bad: Region counts. This
tells you you have excluded all the points not in your selected
region.
- Now type clear region < Enter >
This removes the filter from your image since you pulled out the events you wanted and no longer need the filter.
- Now you must extract the image from those points you selected by
typing:
extract image < Enter >
- Call up SAOimage again to display your new image. (You may close
your old SAOimage window by clicking on etc and then on QUIT or leave it up for comparison with your new display.)
- Getting a Filtered Image
The following is a list of the commands you just used with no comment so that you may refer to it quickly beginning after read events:
extract image < Enter >
saoimage < Enter > (select a region with the cursor)
filter region src.reg < Enter >
extract events < Enter >
clear region < Enter >
extract image < Enter >
saoimage < Enter > (To see the final image)
You may now proceed to manipulate the image of GK PER
The following instructions are optional exercises that demonstrate how you can smooth and average the images using the tools in Xselect. If you choose to try these exercises make sure you return the data to its original form before proceeding to lightcurves and energy spectra. Instructions for restoring the data are part of this exercise, so if you begin these instructions you must follow them through.
- Binning up pixels.
- The image you originally displayed (before the filtering) is made up
of 1024
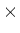 1024 pixels. When you chose the region you simply
selected a particular set of pixels to be displayed. Sometimes,
however, it is helpful to group pixels together into one block to get a
smoother appearence of the data. This technique is called
block-averaging. If you tell Xselect to take every 8 pixels and
replace them with 1 pixel whose grayscale value is the average of
those eight, you have binned up your image into 128
1024 pixels. When you chose the region you simply
selected a particular set of pixels to be displayed. Sometimes,
however, it is helpful to group pixels together into one block to get a
smoother appearence of the data. This technique is called
block-averaging. If you tell Xselect to take every 8 pixels and
replace them with 1 pixel whose grayscale value is the average of
those eight, you have binned up your image into 128 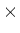 128
pixels. To see this type:
128
pixels. To see this type:
set xybinsize < Enter >
- You will be asked for a rebinning factor (this would be the value 8
mentioned above) select 8 < Enter > to see a 128
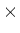 128 pixel image.
128 pixel image.
Then continue to process the image by commanding:
extract image < Enter > and
saoimage < Enter >
You should see your region selected image in a binned up fashion. The pixels should now be larger sized squares.
- Try to rebin with different values such as 32. To do this you simply
need to type:
set xybinsize < Enter > and input the binning you desire.
extract image < Enter >
saoimage < Enter >
The default xybinsize is 15; this means the first image you looked at had an xybinsize of 15. When you are done exploring this function, set it back to 15.
- The image you originally displayed (before the filtering) is made up
of 1024
- Smoothing images.
- Smoothing images often allows you to concentrate on the general
features of the image and not worry about individual pixels.
Type: smooth image < Enter >
You will be asked for a smoothing method. Your options are Boxcar, Gaussian, or Lorentzian. Type Gaussian < Enter > to select this method. You will be asked for a sigma for image smoothing. The default is 1.5 you may accept that value to see what happens.
Again display your result with saoimage < Enter >.
- Notice your object is now smoothed. Try different color schemes on
the smoothed data and pan in on it so you can see it clearer. Notice
the top left part of the image is now bright and there is a dark
``hole'' in the middle. The value 1.5 is the
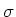 in a gaussian
curve which you are applying to the image, a larger
in a gaussian
curve which you are applying to the image, a larger 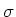 means a
smoother image.
means a
smoother image.
- An image will be smoothed differently depending on the binning factor
of the image. You can explore different possibilities by following
these steps:
set xybinsize < Enter > and input the binning you desire.
extract image < Enter >
smooth image < Enter > then choose Gaussian < Enter > with a
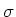 of 2 or any value you wish to explore.
of 2 or any value you wish to explore.
Then view it with saoimage < Enter >.
Try a
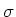 of 3 or 4 to see what happens when you smooth too much!
of 3 or 4 to see what happens when you smooth too much!
- To return the original pixel data set xybinsize 15 < Enter >.
Then type extract image < Enter >. You should saoimage < Enter > just to be sure that your original filtered pixel image is there.
- Smoothing images often allows you to concentrate on the general
features of the image and not worry about individual pixels.
- You will now use the extract command to make a lightcurve of your
observation.
extract curve
- Next you must set a program device upon which your lightcurve can be
plotted.
set device /XW < Enter >
and now plot it plot curve < Enter >
- You will notice that all of your data is in the center of the plot and
a curve or spectrum is hard to make out. Also, notice that at the top
of your plot you are told that the binsize is 16.000s. This means
that the total livetime has been divided into 16s intervals and plotted
accordingly.
Notice on your Xselect screen that the prompt has changed from session1:ROSAT-PSPC> to PLT>. This means you are in an interactive mode with the plot window and commands you give the screen will be received by the plot window.
The most important command is exit; type it if things get really crazy. In this case you can clear events and start the lightcurve extraction all over.
- One useful thing you can do is reset the x and y axes to zoom into
some interesting part of the lightcurve.
rescale x 4e5 6e5 < Enter >
This displays the chosen datapoints across the entire screen. You can zoom in even more by typing rescale x 4.8e5 5.5e5
One notable feature of the PLT
 environment is that you may
an abbreviation of a command, so long as it is unique instead of the
entire string. In this case you can type r x X
environment is that you may
an abbreviation of a command, so long as it is unique instead of the
entire string. In this case you can type r x X X
X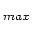 to get the same results.
to get the same results.
Type exit to return to Xselect now.
- It is useful to define a region of interest from your image and
extract the events from that region. Since you already extracted the
lightcurve you can define a time interval through which you can filter
the data.
Type: filter time cursor < Enter >
Again you will be in the PLT> mode. The first thing to do is to enter quit as you are told to do on the screen. Then in the plot itself click to the right of the curve (around x=5.5e5) and to the left (around x=4.8e5). A horizontal line should have connected your clicks.
Then type x in the plot window to exit this mode. NOTE: You can get tangled up very quickly while in this mode. Do not attempt to try the other commands that appear unless you have plenty of time and motivation! The instructions above will be sufficient for your purposes.
- Type show status < Enter > to see that file of the time
selections was added to the filters. It also shows what you have done
so far under PRODUCTS.
- Type extract curve < Enter > since now there has been a filter
applied to it.
And plot curve < Enter >.
- You now have a light curve. You can rescale this curve as you did
before. Typing rescale < Enter > with no argument will return the
original curve.
- Finally, you might want to make a hardcopy (printout) of your
lightcurve. to create a postscript file that can be printed, type at
the PLT> prompt:
filename.ps/PS (make sure there are no spaces in this command) this will make a ps file in your main directory that you can later print out.
- Save your light curve by typing save curve < Enter > and enter a name for your light curve such as gkper_curve < Enter > which will be save by the program under the name gkper_curve.lc
- You will want to make an energy spectrum of the data we have on GKPER.
An energy spectrum contains vital data on the photons that we have collected
from our source - and therefore the photons produced in our
source. You will see that by analyzing and fitting this spectrum to
theoretical curves you can find the temperature of the source, its
luminosity, and information about its chemical composition as well as
its distance.
Type extract spectrum < Enter >
Followed by plot spectrum < Enter >.
You will get a plot of COUNTS vs. CHANNEL
- Look at your plot. The data at the end of your spectrum is not useful
and will affect your analysis later on. You will want to cut out
this data by applying a filter to your spectrum. You should eliminate
data below channel 10 and above cahnnel 300, for example.
filter pha_cutoff < Enter > then enter 10 for the lower cutoff and 300 for the upper cutoff.
Then you must extract spectrum < Enter > and plot spectrum < Enter >.
- Again you will want to save your spectrum by typing save
spectrum < Enter > and entering a name like gkper_spec <
Enter >. The
program will ask you if you want to rebin the data. Enter yes <
Enter >.
Xselect has now saved your extracted energy spectrum under the name gkper_spec.pha. You should plot spectrum one more time to see what the rebinning did.
To better analyze the light curve you extracted, it is useful to make a power spectrum, which is the Fourier transform of the light curve so that you may see the major features of the curve.
- At the prompt type powspec < Enter >. You will be asked to input a
lightcurve file.
You may enter session1_fits_curve.xsl or gkper_curve.lc which is your lightcurve that you saved manually.
- You will be asked for the 'window file'. This is a mask that allows
you to choose various subsets of the data. Choose the default.
- When asked to select newbin time, the program is asking how much time
can it group together into one bin. At first, type in the
default values given. This will bin all the data into one plot or
frame (which allows you to select 1 < Enter > when asked for
the number of intervals/frame).
- Respond to Rebin Results? with 0 < Enter >.
- Select a name for the output file such as gkper.fps < Enter >
- Type yes< Enter > to plot the results.
- Enter your PGPLOT device to be /xw < Enter >.
- Behold the power spectrum!
The axis on you plot should be labeled Power vs. Frequency (Hz) and have the bintime printed at the top right corner. The power spectrum does not show any dominant frequency in the lightcurve. It is mostly noise. This is because our source is weak and because the ROSAT PSPC is only sensitive up to an energy of 1keV. There should be a peak at or around 2.864
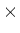 10
10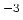 Hz which is a
period of 349 seconds.
Hz which is a
period of 349 seconds.
With a different detector the noisy frequencies would not be present and there would be an obvious peak at the frequency of the source.
Since the detector spans 256 pixels on each axis there are certain factors arising from the detector itself that must be accounted for before further analyzing our data. For each position in the detector there is a certain probability that a photon of a certain energy will be recorded as an event. This probability function (independent of the source we are pointing at) is located in a file that has been created for the ROSAT PSPC named: pspcb_gain2_256.rmf.
The energy spectrum you extracted was plotted in Counts vs. Channel. Each channel on the detector corresponds to an energy. In order to analyze the data properly Xspec must convert the spectrum from Counts vs. Channel to Counts vs. Energy and for this you will need a file named pspcb_v2.spec_resp.
- To retrieve these files you must go back into your Netscape
window. Enter the URL:
http://xray.rutgers.edu/
 matilsky/documents/
matilsky/documents/
- At the top of the netscape screen. A page entitled Index of
 matilsky/documents should appear with a column of links to
various files. With the right mouse button click on pspcb_gain2_256.rmf and select the option Save Link
As...
matilsky/documents should appear with a column of links to
various files. With the right mouse button click on pspcb_gain2_256.rmf and select the option Save Link
As...
In the dialog window that appears, make sure the correct directory to which you want to save these files appears in the Selection box (the same directory with all your GK PER files).
- Click on OK.
- Repeat this for pspcb_v2.spec_resp.
The energy spectrum you extracted in the last step of our Xselect session can be model-fit in a program called Xspec to determine the characteristics of our source. First, however, we must prepare our data to be used in Xspec.
- The task pcarf will make the necessary channel to energy
corrections to your
gkper_spec.pha file.
Type pcarf < Enter > and input gkper_spec.pha < Enter > as your PHA file.
- Next you will be asked for the RMF file explained above. Input pspcb_gain2_256.rmf < Enter > .
- Name the ARF file (which is what this program outputs) gkper.arf< Enter > .
- Enter pspcb_v2.spec_resp < Enter > for the SPECRESP
file.
You have now created all the necessary data files to run an Xspec analysis on GKPER. The next step is to open the Xspec package and fit our data to some spectral models.
- Type xspec < Enter > to call up the package.
- The first thing to do is enter the data into the program. Type data gkper_spec.pha < Enter > .
- Command the program to ignore glaringly bad data points that may be
problematic to a good fit by typing ignore bad < Enter > .
- Next, you should tell the program which plotting device to use to plot
your spectrum.
Type cpd /xw < Enter > (change plotting device).
- Now you must give the program the data it needs regarding the channel
to energy conversion and the ancillary response function we created
using pcarf
Type resp pspcb_gain2_256.rmf < Enter > .
Followed by arf gkper.arf < Enter > .
- To plot your spectrum type plot data < Enter >.
If you type plot ? < Enter > you will get a list off all the things besides your data that you can plot.
- Notice that the plot that appeared is in Counts vs. Channels and it is
similar in shape to the spectrum you extraced from Xselect. To
convert from channels to energy, type setplot energy < Enter >
followed by plot data < Enter >.
It is also possible to use the command plot ldata < Enter > which plots the data with a logarithmic scale on the y-axis.
We will attempt to fit our data to three spectral models:
- Powerlaw spectrum
This model represents a spectrum that arises from a source whose radiating electrons are moving within a magnetic field and therefore experience a force perpendicular to their motion. This torque accelerates the electrons and causes them to radiate in a characteristic way. The spectrum produced by this effect has the mathematical form of a powerlaw where the intensity of the radiation energy is proportional to the energy raised to a power.
I(E)=AE
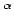
Where:
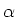 is a spectral index, and
is a spectral index, and
A is a constant.
- Blackbody spectrum
A blackbody spectrum is one that is only dependent on the temperature of the radiating source. This model assumes that the radiating photons get their energy solely from the temperature of the object.
I(E)=2E
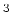 /h
/h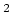 c
c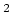 (e
(e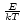 -1)
-1)
Where:
h is Planck's constant, and
c is speed of light.
- Thermal Bremsstrahlung
This radiation spectrum is caused by the thermal motions of electrons in gasses hot enough to be ionized. The presence of charges from the ions exert electromagnetic forces on the electrons that 'bend' their motion and cause them to radiate. The distribution of the energy emitted from such 'bending' depends on the densities of both electrons and ions as well as the temperature of the gas, and it has the form:
A(E)=C
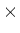 G(E,T) Z
G(E,T) Z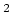 n
n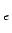 n
n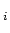 (kT)
(kT)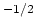 e
e
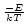
Where:
C is a constant, G(E,T) is a function that varies with temperature and energy, Z is the charge of positive ions in the gas, n
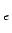 and n
and n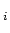 are electron density and positive ion
density, respectively, and T is the temperature.
are electron density and positive ion
density, respectively, and T is the temperature.
- We will enter a powerlaw spectrum first. Type model
phabs(powerlaw) < Enter > or for the abbreviated command (Xspec
accepts truncated commands as long as they are unambiguous) type
mo pha(po) < Enter >.
You will receive a list of parameters that this particular model requires. These parameters are default and we can change them to fit our data with the fit command later. We will accept the default values by pressing < Enter > three times.
The output that follows includes a
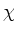
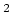 (Chi-Squared) and a reduced
(Chi-Squared) and a reduced
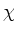
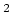 (the original
(the original 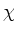
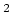 divided by the number of degrees
of freedom). If the reduced
divided by the number of degrees
of freedom). If the reduced 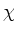
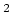 is near 1 then the fit should
be good. The null hypothesis probability is the probability of
getting a value of
is near 1 then the fit should
be good. The null hypothesis probability is the probability of
getting a value of 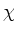
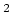 as large or larger than observed if the
model is correct. If this probability is small then the model is not
a good fit.
as large or larger than observed if the
model is correct. If this probability is small then the model is not
a good fit.
- plot data < Enter >
Your fit should be very bad. This is because the model is constructed using the initial default values that do not correspond to your data. Notice that the null hypothesis probability is 0 and that the reduced
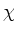
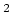 is tens of thousands large. Both of these facts indicate a
poor fit.
is tens of thousands large. Both of these facts indicate a
poor fit.
- You can help the fit by renormalizing your data, you are basically
scaling the model down by multiplying the entire curve by a single
factor determined by your data. Just type renorm < Enter > and
plot data
 < Enter > to see the results.
< Enter > to see the results.
Notice that the right side of the model is attempting to match the slope of the data. Also notice the dramatic reduction in
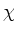
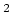 (but still not close to 1).
(but still not close to 1).
- We will now fit our data. The fit command will attempt to match
the parameters of the model to the data. The algorithm goes through
ten iterations at a time attempting to find a minimum
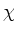
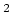 and
prints out the results of the fit.
and
prints out the results of the fit.
Type fit < Enter > and after ten iterations, when prompted to continue fitting type y < Enter >.
- When the fitting is done plot data < Enter > to see the results.
The model does converge to the data though not exactly. To see where the model departs from the data type plot data residuals < Enter >. At the bottom of the screen, the model is represented by the straight line and the data oscillates above and below. It is only toward the higher energies that the residuals shrink and stop oscillating.
Now look at the tabulated results. The reduced
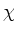
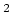 should be
around 6 or 7, which is better than our previous results, but not close
to 1. The null hypothesis probability is tiny as well. This
indicates that our model is not good enough to describe this source
very well.
should be
around 6 or 7, which is better than our previous results, but not close
to 1. The null hypothesis probability is tiny as well. This
indicates that our model is not good enough to describe this source
very well.
In the table (your results may not exactly match but should be close):
--------------------------------------------------------------------------- --------------------------------------------------------------------------- mo = phabs[1]( powerlaw[2] ) Model Fit Model Component Parameter Unit Value par par comp 1 1 1 phabs nH 10^22 0.1122 +/- 0.4740E-02 2 2 2 powerlaw PhoIndex 4.015 +/- 0.1184 3 3 2 powerlaw norm 2.0524E-02 +/- 0.5383E-03 --------------------------------------------------------------------------- ---------------------------------------------------------------------------
Recall that the EXOSAT powerlaw fit gave a column density (nH) of 2.32
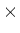 10
10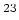 and here we have a column density
1.12
and here we have a column density
1.12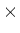 10
10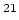 . Two orders of magnitude smaller!
. Two orders of magnitude smaller!
How would you account for this inconsistency?
The reduced
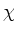
 from this analysis is also closer to 1 than the EXOSAT analysis. This implies that the fit is somewhat better. Are
these signs actual or are they a result of fewer data points (20 vs 57)
that give the illusion of a better fit?
from this analysis is also closer to 1 than the EXOSAT analysis. This implies that the fit is somewhat better. Are
these signs actual or are they a result of fewer data points (20 vs 57)
that give the illusion of a better fit?
Clearly with EXOSAT's wider energy band we are able to show a spectrum with features that the ROSAT data could not reveal - given the 1keV threshold of the PSPC detector.
- Lets try fitting a blackbody spectrum to our data. Type model
phabs(bbody) < Enter> (or mo pha(bb)) and again accept the
default parameters by pressing < Enter > three times.
- plot data < Enter >
Again this is not a good fit and
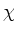
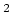 is in the thousands.
is in the thousands.
renorm < Enter > and plot data to scale down the model.
You must now fit < Enter > the model to the data and continue to fit the data by entering y when prompted. When fitting is done, plot data residuals < Enter > to see the deviation from the curve.
This fit is not as good as the power law fit resulting in a reduced
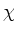
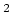 around 14 and an even smaller null hypothesis
probability. The temperature (in units of keV) from the output in kT
is 0.1550 or 1.8E6 Kelvin. This is much lower than the EXOSAT temperature of 3.6
around 14 and an even smaller null hypothesis
probability. The temperature (in units of keV) from the output in kT
is 0.1550 or 1.8E6 Kelvin. This is much lower than the EXOSAT temperature of 3.6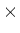 10
10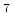 Kelvin.
Kelvin.
Also, note the column density (nH) in this output. The rising function on the left which indicates absorbtion and complicates the fit.
The deviation in column density between models is greater with the ROSAT than with EXOSAT implying a better consitency among the EXOSAT fits. This is probably due to more datapoints from the broader energy range in EXOSAT's detector. The column density here should be around 3.4E20 which is lower than that calculated by the power law model by an order of magnitude.
The presence of the rising function on the left indicates absorbtion and complicates the fit.
- Finally, let's try a thermal bremsstrahlung radiation model. Type
mod pha(bre) < Enter > and accept the initial parameters
as before.
- plot data < Enter >
- renorm < Enter > and plot data < Enter > again.
- fit < Enter > until the fitting is complete. Then plot
data residuals < Enter >.
The results give a better reduced
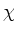
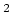 (round 10) and a less
tiny null hypothesis probability, but it seems that the powerlaw fit
was the best one. We can calculate a temperature from here too, and
compare it to the blackbody temperature we calculated earlier. With
an output of 0.3700keV (or something around that value) the
temperature comes out to be 4.3E6 Kelvin. This value agrees at least
to the same order of magnitude, showing that our analysis is
consistent.
(round 10) and a less
tiny null hypothesis probability, but it seems that the powerlaw fit
was the best one. We can calculate a temperature from here too, and
compare it to the blackbody temperature we calculated earlier. With
an output of 0.3700keV (or something around that value) the
temperature comes out to be 4.3E6 Kelvin. This value agrees at least
to the same order of magnitude, showing that our analysis is
consistent.
This temperature and that extracted from the blackbody analysis are lower than the EXOSAT temperature, but there we got completely inconsistent results.
Again the column density changed. This time it increased slightly to about 6.9E20.
None of these fits were good enough, however to provide confident results.
It would be useful to examine how well our data fits the model spectra without the leftmost points indicating absorbtion. This way the fitting process will be 'interacting' with the data points representing photons produced by the processes inside the source and not by the interstellar medium.
- First we must remove any model from our data. Type model none <
Enter > then plot data < Enter >.
- The data is in counts vs. energy. We would like to edit our data to
remove points, it is easiest to do this by converting back to channels.
Type setplot channel < Enter > and plot data < Enter >.
- To neglect the absorbed points use the ignore command and type
ignore 0-15 < Enter >. This commands the program to ignore
channles 0 to 15 in the data. plot data < Enter > again to see
the new dataset. The leftmost point is still sloping down but it is
not certain that it is due to absorbtion, so we will allow it to
remain.
- Now switch back to energy units by typing setplot energy < Enter
> and plot data < Enter >.
- Select a powerlaw model, renormalize, fit, and plot the data.
Did your reduced
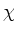
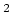 improve from the original powerlaw fit?
improve from the original powerlaw fit?
What is the column density for this data set?
- Repeat the process for blackbody and thermal bremsstrahlung models.
What about these reduced
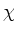
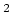 's and column densities?
's and column densities?
Did the temperature output change and if so did it go up or down? why?
Was the change in temperature as significant as that of the column density?
- Now that you have done the analysis for each model, twice, and have
looked at the data with and without absorbtion, which model fit your
data best?
Type flux < Enter >. You will receive an output showing the
flux of the star in photons/cm![]() /s and in ergs/cm
/s and in ergs/cm![]() /s. Once you
know the flux and the distance to the source, you can know its
luminosity.
/s. Once you
know the flux and the distance to the source, you can know its
luminosity.
How did the flux here compare with EXOSAT? Why?