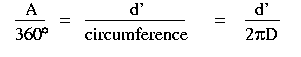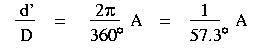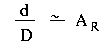SIZES AND DISTANCES
The Small Angle Approximation
It is quite remarkable that by using a circle, we can easily figure out
distances in the sky! To understand how this works, we first
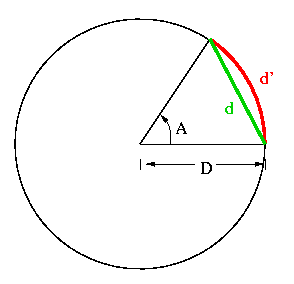
examine the pciture below. Just as an angle of a circle, A,
represents a fraction of the full circle, (360 degrees), so the length
of arc, d', subtended by the angle A is a fraction of the
circumference of the full circle. In the diagram below, the
radius of the
circle is D and the length of the arc subtending the angle A is d'.

From this diagram we see that the following ratios are equal
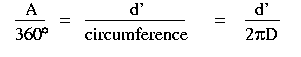
We can rewrite this equation as
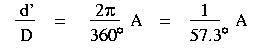 We are free to define "A" in any way we choose! To make the arithmetic
simpler, we define A = 57.3 degrees as
the unit of angular measure, the radian. By measuring angles in
radians, AR, we can write
We are free to define "A" in any way we choose! To make the arithmetic
simpler, we define A = 57.3 degrees as
the unit of angular measure, the radian. By measuring angles in
radians, AR, we can write

That is, for AR = 0.1, D = 10d (and A = 5.73
degrees).
All other angles can be obtained similarly! For example, if A= 10
degrees, then AR is about one-sixth.
This simple relationship becomes quite useful and powerful when we
consider a
straight line segment of length d (a chord) connecting the two ends of
the arc of length
d'.
As A becomes smaller, the chord length d becomes a better
approximation to the arc length d', that is, d ~ d'. Therefore, we may
write:
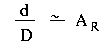
This is the small-angle approximation. It correctly relates the length
of the sides of a long, skinny triangle.
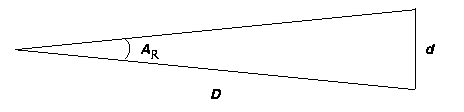
Long skinny triangles have many applications. Suppose d
is the diameter of the Moon in miles and D is the
distance from the Earth to the Moon in the same units. Then AR
is the angular size of the Moon as viewed from the Earth.* If we know two of these three quantities, we
can use the long skinny triangle relation to solve for the third.
*But remember, AR is expressed
in radians, where one
radian = 57.3 degrees. For the Moon, A = 0.5 degrees and AR
= 0.5/57.3 = 0.0087. radians
Last updated on:
Thu, 09 Nov 2000 04:33:17 GMT