Go back to the top.
Coordinate Systems
It’s the year 2006, and the amazing astronomers at NASA have done it again.
They have made star travel, once only seen in science fiction movies, a reality. No more day dreaming
about flying with Han in space. We have our own ship and it is a hundred times
better than the Millennium Falcon. The only problem is that not many people know
their way around space yet. How can we ever learn how to travel in space if we
haven’t the faintest idea where the objects are in relation to each other? Luckily,
the ingenious scientists have developed a system to relate the objects in space to
each other. Let’s take their course on coordinate systems so we can get flying in
outer space!
Some of you may be asking what exactly are coordinate systems? Actually,
most of you probably know more than you think. We use coordinate systems all
the time on Earth. We can graph equations on the x-y coordinate system, we can
read a map and determine how to get to our final destination, and we are all familiar
with the latitude and longitude lines that we drawn on maps of the Earth. But how
do we map the universe?
For more information on coordinate systems click on this picture of the Earth to access a website designed by
Peter H. Dana The Geographer's Craft Project, Department of Geography, The University of Colorado at Boulder.
Just like on the Earth, we use coordinate systems! Click on the "coordinate system" below to learn more.
Now that you have learned a bit about Galactic coordinates. Answer the questions below.
Choose all of the possible answers.
The galactic plane is analogous to the
Prime Meridian
Equator
Tropic of Capricorn
Tropic of Cancer
The center of the galaxy allows us to define the
Prime Meridian
Equator
Tropic of Capricorn
Tropic of Cancer
How is the coordinate system used for the universe more complicated than the
coordinate system used for the Earth? (Hint: Think about the space the Earth occupies).
Can you think of a disadvantage of plotting the universe on a map like the one above?
Okay, so now we know how we can map the objects in space on a map. But how can
we determine how far the objects are from Earth? Easy, we just have to interpret the map.Look at the pictures below. Take note of the galactic coordinates.
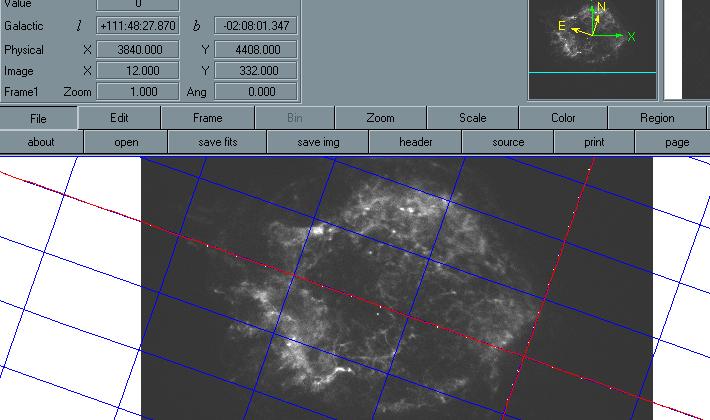
The picture above is of Cassiopeia A.
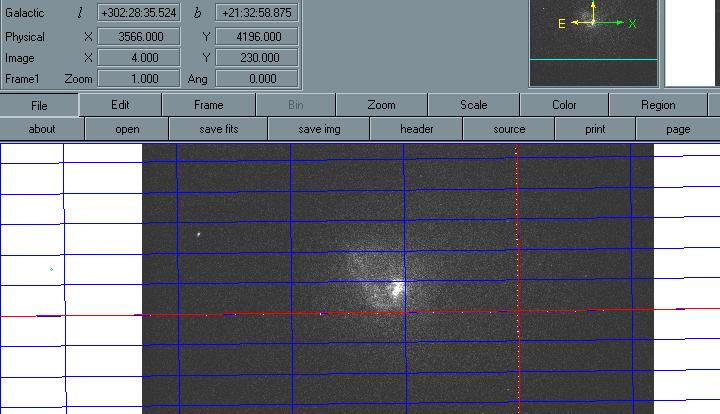
The picture above is of the Large Magellanic Cloud Pulsar.
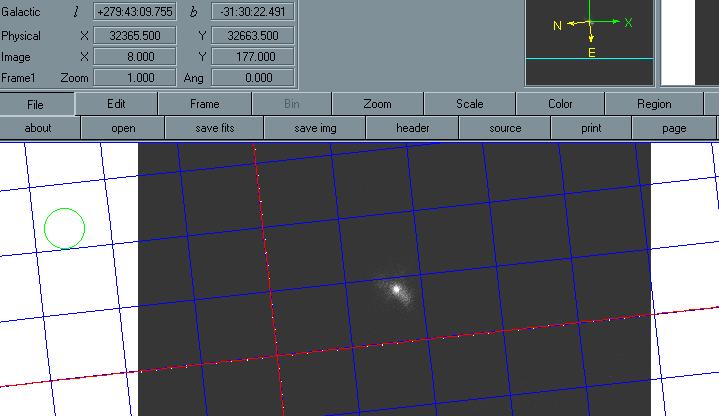
The picture above is of the Centaurus Cluster.You may have noticed that the galactic coordinates are (l , b). These coordinates are in degrees, minutes, and seconds of arc. These coordinates are written in the form 00:00:00.000 and have either a positive or a negative sign. However, only the b coordinate, the galactic latitude will be negative. Remember the galactic longitude plane (l) starts at 0o and ends at 360o. On the other hand, the b coordinate, on the galactic latitude, starts at -90o at the South Celestial Pole and goes to 90o at the North Celestial Pole. Remember the Earth is at 0o latitude.
From the pictures above, we found the following:
Object Galactic Latitude (b) Galactic Longitude (l)
Cas-A 111:48:27.870 -02:08:01.347
Large Magellanic Cloud 302:28:35.524 +21:32:58.875
Centaurus Cluster 279:43:09.755 -31:30:22.491
To determine the degrees for the galactic coordinates, one must convert the minutes and the seconds of arc to degrees.
There is 1 degree in 60 minutes of arc and 60 seconds of arc in one minute of arc.Determine the galactic coordinates in degrees.
Object Galactic Latitude (b) Galactic Longitude (l)
Cas-A
Large Magellanic Cloud
Centaurus Cluster
Using these values we can convert the galactic coordinates into geocentric coordinates. Geocentric means "Earth-centered." These coordinates have the Earth's center as their origin. In astronomy the geocentric coordinates are called the equatorial coordinates. This system consists of right ascension,
and declination,
.
The galactic coordinates can be converted into equatorial coordinates using the following equations:
sin
cos
cos
Now use the relationships above to determine the equatorial coordinates.Object Declination (
Cas-A
Large Magellanic Cloud
Centaurus Cluster
From these results, can you determine which object is the closest to the Earth? Which object is the farthest?
As you can see on the picture above, l is the galactic longitude and b is the galactic latitude.So now you are thinking, “Okay, I know about galactic coordinates, I can determine
how far objects are in the sky, but what if I want to get somewhere in space? How do
I find the galactic coordinates?” Don’t worry, determining the galactic coordinates is as
easy as obtaining directions on MapQuest. Unfortunately, you will have to determine the
best route to get to your destination. Hey, I never said being a pioneer was easy. But don’t
worry you shouldn't run into too many meteors.
First, load the Chandra image that you are interested in and the analysis software into Ds9.
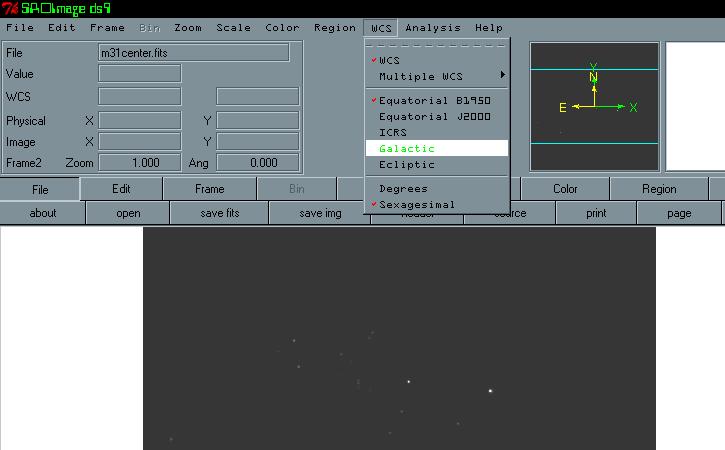
Next go to the “WCS” option on the toolbar. Scroll down and choose “Galactic”.
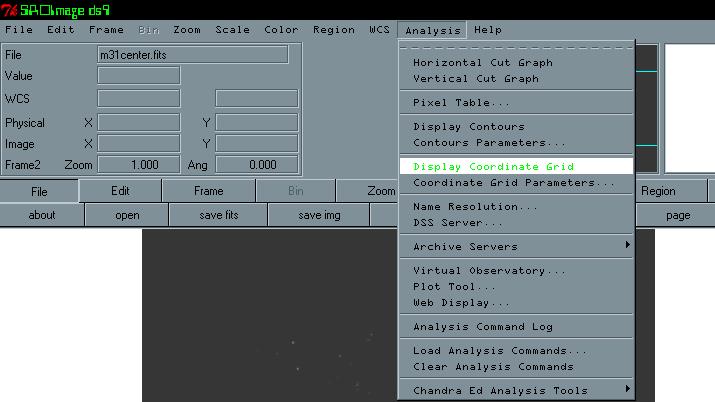
Next, go the “Analysis” option on the toolbar and choose “Display Coordinate Grid”.
When you click on “Display Coordinate Grid,” gridlines should appear that are similar to
the image below. When you move the mouse to the red line the galactic coordinates (l, b) will appear.
You have just found the galactic coordinates. Now it is time for the interpretation.
Go back to the top.
