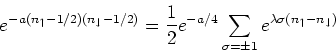
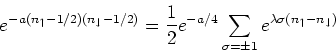
where
![]() (Hint: consider the matrix representation of the operator
on the left hand side in the four dimensional Fock space of the up and down electrons.)
We shall later see how, considering
(Hint: consider the matrix representation of the operator
on the left hand side in the four dimensional Fock space of the up and down electrons.)
We shall later see how, considering
![]() to be an infinitesimal time interval,
we can use this relation to treat interacting spins as spins moving in a fluctuating Ising
magnetic field.
to be an infinitesimal time interval,
we can use this relation to treat interacting spins as spins moving in a fluctuating Ising
magnetic field.