BALLISTIC PENDULUM

Name:                                                                  Section:                   

Partner:                                                                  Date:                   

A. Ballistic Pendulum:

Table 1: Basic Data

mass of ball	$m$
mass of catcher	$M$
Center of Mass (C.M.) initial height at rest	$h_{\rm initial}$

Table 2: Data on C.M. height change

Trial #	Final C.M. height = $h_{\rm final}$	$h = h_{\rm final} - h_{\rm initial}$
1
2
3
4
5

Mean height $\overline{h}$:                                    $\sigma_h$ (S.D.):                               

Recall that $\sigma_h$ = standard deviation (S.D.) of an individual measurement:

$$\sigma_h = \sqrt{\frac{\sum_{i=1}^{N} (h_i-\overline{h})^2}{N-1}}$$

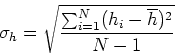
B. Projectile Range

Distance from spring plunger end to paper edge $x_0 =$                                m.

Table 3: Data on projectile range

Trial #	Distance on Paper $\delta$ (m)	Total horizontal distance $x = x_0 + \delta$
1
2
3
4
5

Initial height of the ball above the floor and the estimated error:

$y =$                                    $\Delta y =$                                m.

Problem 1 Using eqns. (7) and (8) and your ballistic pendulum data calculate the predicted horizontal distance the ball will travel and the error. Compare your predictions with the measured projectile range. Discuss any differences.

Table 4: Comparison of predicted and measured horizontal range values

Predicted		Measured
$X$		$\overline{x}$
$\Delta X$		$\sigma_{x}$
$X+\Delta X$		$\overline{x}+\sigma_{x}$
$X-\Delta X$		$\overline{x}-\sigma_{x}$

Because $y$ is constant, we expect the variation in the distance traveled to be given by the variation in $h$, i.e., $\Delta x=(\Delta h/h)x$. With this interpretation, what percentage of the measured trajectories would you predict to fall within the predicted range? What percentage actually do?

Problem 2 Calculate the ball's initial horizontal velocity, $v_{x0}$, from eqn. (6). Convert to mi/hr. (1 mile = 1609 meters = 5280 ft; g=32 ft/s$^2$=9.8 m/s$^2$). How does this compare to the speed of a pitched baseball (about 90 mph for a fastball).

Problem 3 In the Introduction the statement is made ``Once the catcher-swing starts in motion, conservation of mechanical (kinetic plus potential) energy applies because the force of the swing-arm is always perpendicular to the motion of the catcher.'' Explain more fully what this statement means.