STANDING WAVES

Name:                                                                  Section:                   

Partner:                                                                  Date:                   

A. Transverse Waves: $\rho = 2\times 10^{-4}$ kg/m; driving frequency, $f =$                    Note that $F$ denotes force while $f$ denotes frequency. $\lambda/2$ equals the number of half wavelengths, i.e., $L$/# of half waves.

Table: Results for tension value: $F_1 =$                                       

$L$	$n$	$\lambda/2$	$c_{\rm exp}$
vibrating length	# half-waves in $L$	$(L/n)$	$(f\lambda)$

$\overline{c_{\rm exp}} =$                                     $\pm$                                      . (Explain how you estimated the error here.)

Theoretical wave velocity, $c_{\rm th} = \sqrt{F/\rho}$, $c_{\rm th} =$                                     (show calculation).

Table: Results for tension value: $F_2 =$                                       

$L$	$n$	$\lambda/2$	$c_{\rm exp}$
vibrating length	# half-waves in $L$	$(L/n)$	$(f\lambda)$

$\overline{c_{\rm exp}} =$                                     $\pm$                                      .

$c_{\rm th} =$                                     (show calculation).

Table: Results for tension value: $F_3 =$                                       

$L$	$n$	$\lambda/2$	$c_{\rm exp}$
vibrating length	# half-waves in $L$	$(L/n)$	$(f\lambda)$

$\overline{c_{\rm exp}} =$                                     $\pm$                                      .

$c_{\rm th} =$                                     (show calculation).

For the three tensions compare the estimated error with the percent discrepancy between $c_{\rm th}$ and $\overline{c_{\rm exp}}$. Is there any error in $c_{\rm th}$? Can you conclude that your measurements agree with theory? Discuss

B. Longitudinal Waves: Temperature:             

Frequency $f_1 =$                   

Positions of intensity maxima (i.e., location of anti-nodes):

1:                2:                3:                4:                5:                6:              

Take the difference between successive maxima to get $\lambda/2$ values:

2$-$1:                3$-$2:                4$-$3:                5$-$4:                6$-$5:              

Average wavelength, $\overline{\lambda}=$                      

Experimental wave velocity, $c=f\lambda=$                       $\pm$                       .

Theoretical wave velocity, $331.4+0.6T_{\rm C} =$                      

Frequency $f_2 =$                   

Positions of intensity maxima (i.e., location of anti-nodes):

1:                2:                3:                4:                5:                6:              

Take the difference between successive maxima to get $\lambda/2$ values:

2$-$1:                3$-$2:                4$-$3:                5$-$4:                6$-$5:              

Average wavelength, $\overline{\lambda}=$                      

Experimental wave velocity, $c=f\lambda=$                       $\pm$                       .

Theoretical wave velocity, $331.4+0.6T_{\rm C} =$                      

Frequency $f_3 =$                   

Positions of intensity maxima (i.e., location of anti-nodes):

1:                2:                3:                4:                5:                6:              

Take the difference between successive maxima to get $\lambda/2$ values:

2$-$1:                3$-$2:                4$-$3:                5$-$4:                6$-$5:              

Average wavelength, $\overline{\lambda}=$                      

Experimental wave velocity, $c=f\lambda=$                       $\pm$                       .

Theoretical wave velocity, $331.4+0.6T_{\rm C} =$                      

From the air column data, what can you conclude about the dependence of the speed of sound on frequency ? Make sure you have the evidence to support your conclusion.

From your data what can you say about whether the loudspeaker is a node or anti-node? Explain (think carefully about this - the microphone detects pressure not displacement).

Your lab write-up will consist of the original data sheets with questions answered along with the following:

For part A (vibrating string), take the uncertainty in $\rho$ to be $2 \times 10^{-5}$ kg/m (i.e., 10% of the nominal value) and find the uncertainty in the theoretical velocity. Assume the uncertainty in the experimental velocity comes only from the uncertainty in the wavelength (i.e., you may neglect the uncertainty in the force and frequency). Take the total uncertainty to be $\sigma_{\rm tot} = \sqrt{\sigma_{\rm th}^2 + \sigma_{\rm exp}^2}$ and express the difference between the theoretical and experimental velocities in terms of $\sigma_{\rm tot}$. A difference of less than $2\sigma_{\rm tot}$ means they agree. Show your calculations and comment on the agreement of theory and experiment.

For part B assume the uncertainty in the frequency is equal to the smallest unit shown on the function generator (i.e., if the frequency is 4.05 kHz, take the uncertainty to be 0.01 kHz). Compare the uncertainty in the velocity due to the uncertainty in the frequency with the uncertainty in the velocity due to the uncertainty in the distance. Be sure to measure distances to the closest mm. Find the uncertainty in the distance use the usual formula of

$$\sigma = \sqrt{\frac{\sum_{i=1}^{N} (x_i-\overline{x})^2}{N-1}}.$$

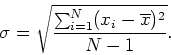
Again, show your calculations and comment on the agreement.