| (1) |
PURPOSE:
To understand terminology and concepts used in measurement.
To apply these concepts in a simple experimental situation.
To become familiar with the use of a spreadsheet.
READINGS:
Baird, 2.1 to 2.7, 2.11, and 3.1 to 3.11
APPARATUS:
Gate generator
Timer
INTRODUCTION:
For a scientist to arrive at a valid conclusion in testing a theory or hypothesis it is necessary to understand the underlying concepts of measurement errors. In engineering and manufacturing these same concepts are important in designing and making quality products.
Systematic errors are those which would tend to reproduce the same incorrect answer if the experiment were repeated using the same techniques. Instruments can generate systematic errors by erroneous design or construction. A ruler with a worn end or a voltmeter whose pointer has been bent are simple examples. Or, the experimenter can introduce a certain bias. The accuracy of an experiment is limited by systematic errors. You cannot improve the accuracy of an experiment by repeating it a number of times and taking the average; the systematic error will not average away.
A random error is one which tends to produce different results when an experiment is repeated using the same technique. The average of a large number of such repetitive measurements will reduce random error by averaging out the variation: the measured value will sometimes be above the actual value and sometimes below. Experimental precision is limited by random errors.
MATHEMATICAL DESCRIPTION OF RANDOM ERRORS
The first important concept is the average (arithmetic mean) of a number of
measurements:
| (1) |
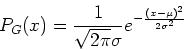 |
(2) |
In this plot the vertical scale is the number of times a given value
of ![]() is measured. The horizontal scale is the value of
is measured. The horizontal scale is the value of ![]() expressed in
units of
expressed in
units of ![]() , the standard deviation, which is a measure of the spread
of the measured values of
, the standard deviation, which is a measure of the spread
of the measured values of ![]() . The mathematical expression for
. The mathematical expression for ![]() is given by:
is given by:
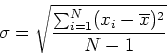 |
(3) |
There is a second closely related quantity -
![]() , the
standard deviation of the mean of the measurement of
, the
standard deviation of the mean of the measurement of ![]() -
that is frequently confused with
-
that is frequently confused with ![]() .
.
![]() gives an estimate of the uncertainty in the measurement of the
mean. Mathematically,
gives an estimate of the uncertainty in the measurement of the
mean. Mathematically,
![]() is given by:
is given by:
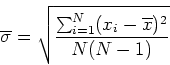 |
(4) |
To illustrate the procedure we will work out the average (mean) value
![]() and the standard deviation of the mean,
and the standard deviation of the mean,
![]() , and the standard deviation of an individual data
point,
, and the standard deviation of an individual data
point, ![]() , using the position measurements in the
accompanying Table 1.
, using the position measurements in the
accompanying Table 1.
| |
|
|
|---|---|---|
| 15.68 | 0.15 | 0.0225 |
| 15.42 | -0.11 | 0.0121 |
| 15.03 | -0.50 | 0.2500 |
| 15.66 | 0.13 | 0.0169 |
| 15.17 | -0.36 | 0.1296 |
| 15.89 | 0.36 | 0.1296 |
| 15.35 | -0.18 | 0.0324 |
| 15.81 | 0.28 | 0.0784 |
| 15.62 | 0.09 | 0.0081 |
| 15.39 | -0.14 | 0.0196 |
| 15.21 | -0.32 | 0.1024 |
| 15.78 | 0.25 | 0.0625 |
| 15.46 | -0.07 | 0.0049 |
| 15.12 | -0.41 | 0.1681 |
| 15.93 | 0.40 | 0.1600 |
| 15.23 | -0.30 | 0.0900 |
| 15.62 | 0.09 | 0.0081 |
| 15.88 | 0.35 | 0.1225 |
| 15.95 | 0.42 | 0.1764 |
| 15.37 | -0.16 | 0.0256 |
| 15.51 | -0.02 | 0.0004 |
From the above table we can make the following calculations:
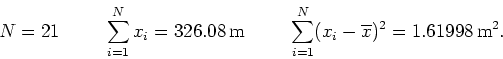
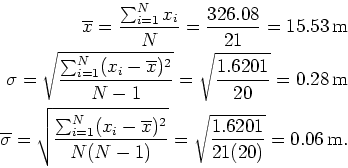
The error or spread in individual measurements is ![]() m. But for the mean
m. But for the mean
![]() m. This says the average is 15.53 m which has an error of 0.06
m. Or putting it another way, there is about a 68% probability that
the true value of
m. This says the average is 15.53 m which has an error of 0.06
m. Or putting it another way, there is about a 68% probability that
the true value of ![]() falls in the range 15.47 m to 15.59 m. In some
cases the fractional error
falls in the range 15.47 m to 15.59 m. In some
cases the fractional error
![]() , or relative
error, is of more interest than the absolute value of
, or relative
error, is of more interest than the absolute value of ![]() . It is
possible that the size of
. It is
possible that the size of ![]() is large while the fractional error
is small. Note that increasing the number of individual measurements
on the uncertainty of the average reduces the statistical uncertainty
(random errors); this improves the ``precision''. On the
other hand, more measurements do not diminish systematic
error in the mean because these are always in the same direction; the
``accuracy'' of the experiment is limited by systematic errors.
is large while the fractional error
is small. Note that increasing the number of individual measurements
on the uncertainty of the average reduces the statistical uncertainty
(random errors); this improves the ``precision''. On the
other hand, more measurements do not diminish systematic
error in the mean because these are always in the same direction; the
``accuracy'' of the experiment is limited by systematic errors.
In today's experiment you will compare three data sets measuring reaction times - two sets will be on your own reaction time and one on your partner's. You will determine whether the last two data sets are significantly different from the first. In order to be clear about the purpose of the experiment, let's go through the reasoning for a concrete example unrelated to the experiment:
Suppose the students in a class are randomly assigned to one of three
groups, each with ![]() students, and two groups are taught some new
material using one teaching technique, while the third group is taught
the same material using a different technique. The three groups are
then given the same exam on the material. We'll call the average exam
scores for the three groups
students, and two groups are taught some new
material using one teaching technique, while the third group is taught
the same material using a different technique. The three groups are
then given the same exam on the material. We'll call the average exam
scores for the three groups
![]() ,
,
![]() , and
, and
![]() , and the standard deviations of the means
, and the standard deviations of the means
![]()
![]() , and
, and
![]() .
.
We would expect the difference to be ``small'' since the same the two
groups were taught the same way and we would like to attribute the
difference to just random measuring errors. On the other hand, in
order to say that the two different teaching methods produce different
learning results we need to be able to say that
![]() is ``large''. But small or large compared to
what? The answer is - small or large compared to the error in
determining
is ``large''. But small or large compared to
what? The answer is - small or large compared to the error in
determining
![]() (or
(or
![]() ), which we'll call
), which we'll call ![]() (or
(or ![]() ). You calculate these errors from the standard
deviations of the mean as follows:
). You calculate these errors from the standard
deviations of the mean as follows:
![]() and
and
![]() . If groups 1
and 2 are not different then there is a 68.3% probability that
. If groups 1
and 2 are not different then there is a 68.3% probability that
![]() will be less than or equal to
will be less than or equal to
![]() , a 95.4% that it will be less than/equal to
, a 95.4% that it will be less than/equal to
![]() , and a 99.7% that it will be less than/equal to
, and a 99.7% that it will be less than/equal to
![]() . The scientific convention is to say
two measurements are significantly (or statistically)
different if they differ by three standard deviations or more. Thus
we say that groups 1 and 2 are not significantly different provided
. The scientific convention is to say
two measurements are significantly (or statistically)
different if they differ by three standard deviations or more. Thus
we say that groups 1 and 2 are not significantly different provided
![]() .
Likewise, groups 1 and 3 are significantly different if
.
Likewise, groups 1 and 3 are significantly different if
![]() . Notice that
. Notice that
![]() (like
(like
![]() and
and
![]() )
gets smaller as
)
gets smaller as ![]() , the number of students, increases. Thus if one
teaching technique produces a large improvement in learning, you will
only have to try the experiment out on a small group of students to
prove there is a significant difference. If there is only a small
difference in learning, you will have to use a very large
, the number of students, increases. Thus if one
teaching technique produces a large improvement in learning, you will
only have to try the experiment out on a small group of students to
prove there is a significant difference. If there is only a small
difference in learning, you will have to use a very large ![]() to
determine if the difference is significant.
to
determine if the difference is significant.
PROCEDURE
In this experiment you will take two sets of data on your reaction time and compare the two sets to see if there is a significant difference between them. Then you will compare one set of your data with that of your partner. We will provide you with an automatic light and timer. The light will flash on after being off for a random time. The light starts a digital timer with 0.001 second resolution. You stop the timer by depressing the switch as soon as you see the light. This turns off the light. The timer will then show your reaction time - the time it takes for you realize that the light has come on and to react by pushing the stop button. There is a reset button to zero the display after you record the time. After a random time (on the order of 10 seconds) the flasher once again turns on the light and starts the clock.
Histograms can be made using the FREQUENCY function in Excel. It has the form frequency(data array, bins array). For example, frequency(a1:a10,b1:b20) would bin the data in a1 through a10 according to the bins listed in bins b1 through b20. In order to enter the function, highlight the area where the results should be displayed, type the frequency call desired (e.g., frequency(a1:a10,b1:b20)), then hit Control-Shift-Enter (PC) to enter the call. For example, the bins array might be as follows: b1 = blank, b2=5, b3=6, b4=7. Highlight the region c1 to c4. After entering frequency, cell c1 will have the number of values in the data array less than or equal to 5, c2 will have the number greater than 5 and less than or equal to 6, c3 greater than 6 and less than or equal to 7, and c4 the number greater than 7.
Significant Figures
Be sure to read section 2.11 in Baird on significant figures and quote
all results accordingly. In general, the uncertainty is quoted to
only one significant figure unless that is a 1, in which case it is
sometimes quoted to two (i.e., 0.3, not 0.33, but 0.1 or 0.13
would be acceptable). The value should be quoted to the same precision
as the error, or at most one more. For example, give ![]() not
not
![]() and not
and not ![]() , although
, although ![]() or
or
![]() would be acceptable.
would be acceptable.