ERROR ANALYSIS

Name:                                                                  Section:                   

Partner:                                                                  Date:                   

Comparison of your average reaction times and standard deviations.

Table 1: Data on Your Reaction Time

Run # 1			Run # 2
$t_i$	$t_i - \overline{t}$	$(t_i - \overline{t})^2$	$t_i$	$t_i - \overline{t}$	$(t_i - \overline{t})^2$
$\sum_{i=1}^{N} t_i$	$\sum_{i=1}^{N} (t_i - \overline{t})$	$\sum_{i=1}^{N} (t_i - \overline{t})^2$	$\sum_{i=1}^{N} t_i$	$\sum_{i=1}^{N} (t_i - \overline{t})$	$\sum_{i=1}^{N} (t_i - \overline{t})^2$

Enter in mean times and standard deviations for each.

$\overline{t_1} =$                            $\overline{t_2} =$                            $\mid \overline{t_1} - \overline{t_2} \mid =$                      

$\sigma_1 =$                            $\sigma_2 =$                      

$\overline{\sigma_1} =$                            $\overline{\sigma_2} =$                            $\sqrt{\overline{\sigma_1}^2 + \overline{\sigma_2}^2} =$                      

Compare your reaction times for the two runs.

$$R_{12} = \frac{\mid \overline{t_1} - \overline{t_2} \mid} {\s... ... \overline{\sigma_2}^2}} = \underline{                      }$$

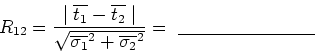
Reaction time of your partner:

Table 2: Data on Partner's Reaction Time

$t_i$	$t_i - \overline{t}$	$(t_i - \overline{t})^2$
$\sum_{i=1}^{N} t_i$	$\sum_{i=1}^{N} (t_i - \overline{t})$	$\sum_{i=1}^{N} (t_i - \overline{t})^2$

Calculate your partner's reaction time.

$\overline{t_3} =$                            $\sigma_3 =$                            $\overline{\sigma_3} =$                      

Compare reaction times for you and your partner.

$$R_{13} = \frac{\mid \overline{t_1} - \overline{t_3} \mid} {\s... ... \overline{\sigma_3}^2}} = \underline{                      }$$

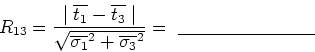
1. Write a short paragraph on the conclusions you can draw from $R_{12}$ and $R_{13}$.

2. Compare the variability of the individual reaction time measurements for you and your partner. Who has the ``steadier nerves'' (i.e., smallest deviation)?

3. Use $\overline{t_1}$ to calculate how far your car travels at 50 mph before you hit the brakes after you see a traffic light change. (1 mi = 5,280 ft = 1610 m). This is the mean ``reaction distance''; that is, the distance it takes you to react. Your brakes can stop your car in 180 feet once you apply the brakes. What is the maximum and minimum distances (at a 95.4% confidence level) that you will travel before stopping after the light changes. Show your reasoning and analysis . Based on this, how much distance should you leave between you and the car in front of you when traveling at 50 mph.

4. Combine the two sets of data for $t_1$ and $t_2$ to give a data set of 20 measurements. Use Microsoft Excel to calculate $\overline{t}$, $\sigma$, and $\overline{\sigma}$. Use the plotting feature of Excel to make a histogram of the data. Pay careful attention to choosing a proper bin size. Indicate the ranges $\pm\sigma$, $\pm2\sigma$, etc., on the histogram and determine the percent of the measurements falling within these ranges.