PURPOSE: To study the relationships of displacement, velocity, acceleration, kinetic energy, potential energy, amplitude and frequency in simple harmonic motion, and to explore the effects of non-linearity on these relationships.
APPARATUS: Computer, universal lab interface, spring, weights, Interactive Physics software
INTRODUCTION: There are many cases in nature where an object oscillates. An oscillation is a swinging or vibrating motion. As the object moves away from its rest position, there is a force that opposes the displacement, forcing the object back. This force, called the restoring force, tries to return (restore) the object to the rest position. However, the object overshoots, and the force then acts in the opposite direction pushing the object back. If there is no loss of energy, the oscillation continues indefinitely.
When the restoring force is opposite and directly proportional to the displacement, the oscillating object will exhibit Simple Harmonic Motion, SHM. The object is called a Simple Harmonic Oscillator, SHO.
Oscillating Spring: As an example of a SHO, let's consider a mass,
![]() , attached to a spring which is fixed at one end and free to slide
on a frictionless surface. Mathematically, the restoring force exerted
by the spring on the mass is given by Hooke's law,
, attached to a spring which is fixed at one end and free to slide
on a frictionless surface. Mathematically, the restoring force exerted
by the spring on the mass is given by Hooke's law,
| (1) |
The constant ![]() , called the spring constant, characterizes the
stiffness of the spring. A large
, called the spring constant, characterizes the
stiffness of the spring. A large ![]() means a large force is needed to
stretch (or compress) the spring a small distance.
means a large force is needed to
stretch (or compress) the spring a small distance.
The rest position is at ![]() where the force is zero. The force on
the mass reaches a maximum at
where the force is zero. The force on
the mass reaches a maximum at ![]() , where the mass momentarily
stops and then moves back toward its rest position.
, where the mass momentarily
stops and then moves back toward its rest position. ![]() is called the
amplitude of the oscillation.
is called the
amplitude of the oscillation.
By conservation of energy, the total mechanical energy of a SHO is constant,
When the spring is stretched to its maximum, ![]() , and the velocity,
, and the velocity, ![]() ,
is zero, so the total mechanical energy is
,
is zero, so the total mechanical energy is
For any other position of the spring, ![]() and
and ![]() are related through
are related through
| (2) |
Then, solving this equation for ![]() , the velocity as a function of the
displacement,
, the velocity as a function of the
displacement, ![]() , is
, is
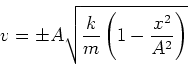 |
(3) |
The SHO moves back and forth, so its velocity will be either in the plus
or minus direction, but the velocity's magnitude depends only on the
magnitude of ![]() . Next, we want to derive an expression for how the
displacement varies with time,
. Next, we want to derive an expression for how the
displacement varies with time, ![]() . Substituting Eqn. (1) and the
definition of acceleration,
. Substituting Eqn. (1) and the
definition of acceleration, ![]() , into Newton's
second law,
, into Newton's
second law, ![]() , we get:
, we get:
| (4) |
This is a differential equation that you may not have yet learned how
to solve.Fortunately, any way you get a solution is fine. We'll
``guess'' that the solution is
| (5) |
where ![]() is the period of the oscillation, the time it takes
for the mass to complete one cycle of oscillation. We check that our
``guess'' is right by substituting Eqn. (5) into Eqn. (4), and find
that it a solution, provided the period is related to
is the period of the oscillation, the time it takes
for the mass to complete one cycle of oscillation. We check that our
``guess'' is right by substituting Eqn. (5) into Eqn. (4), and find
that it a solution, provided the period is related to ![]() and
and ![]() by
the relation:
by
the relation:
| (6) |
The frequency (usually expressed in Hertz) of the SHO's
oscillations is
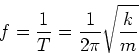 |
(7) |
Substituting Eqn. (6) into Eqn. (5) we get,
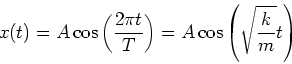 |
(8) |
Note that this solution assumes that at ![]() ,
, ![]() ; the SHO
starts at the positive amplitude. The velocity as a function of time
is found by taking a derivative with respect to time,
; the SHO
starts at the positive amplitude. The velocity as a function of time
is found by taking a derivative with respect to time, ![]()
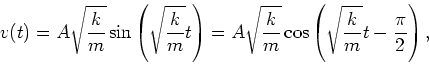 |
(9) |
where we have used the identity:
![]() .
The acceleration,
.
The acceleration, ![]() , is
, is
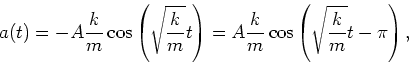 |
(10) |
where we have used the identity:
![]() .
.
Simple pendulum: As a second example of an oscillating system,
let us study the simple pendulum - a mass attached to light string
and swinging from side to side, as shown in the accompanying figure 1.
The only two forces acting on the mass are the tension ![]() in
the string and the weight
in
the string and the weight ![]() . The tension is partly balanced by the
component
. The tension is partly balanced by the
component
![]() of the weight. The sum of these forces
produces the inward (centripetal) acceleration as the ball moves in a
circle. The other component of the weight is
of the weight. The sum of these forces
produces the inward (centripetal) acceleration as the ball moves in a
circle. The other component of the weight is
![]() ,
where the minus sign indicates that
,
where the minus sign indicates that ![]() is acting opposite to the
displacement,
is acting opposite to the
displacement, ![]() , where
, where ![]() is the arc length. This force
accelerates the mass along the circumference of the circle toward
is the arc length. This force
accelerates the mass along the circumference of the circle toward
![]() and produces SHM. If we assume that
and produces SHM. If we assume that ![]() is small,
then
is small,
then
![]() and we can write the restoring force
as:
and we can write the restoring force
as:
| (11) |
Comparing this equation to Eqn. (1) shows that we again have Hooke's
law with the displacement now being the arc length ![]() instead of
instead of ![]() and with
and with ![]() . Then we can immediately see, using Eqn. (6),
that the period of the (simple) pendulum is
. Then we can immediately see, using Eqn. (6),
that the period of the (simple) pendulum is
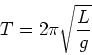 |
(12) |
In this lab you will use Interactive Physics to simulate the
simple pendulum to verify this relationship and then explore how
the period changes for large oscillations when ![]() is no
longer small and the restoring force is no longer simply proportional
to
is no
longer small and the restoring force is no longer simply proportional
to ![]() . You may also want to explore the behavior of the physical pendulum,
where the oscillating object is not a point mass but an extended body.
In that case the period becomes:
. You may also want to explore the behavior of the physical pendulum,
where the oscillating object is not a point mass but an extended body.
In that case the period becomes:
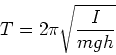 |
(13) |
where ![]() is the moment of inertia of the body about the pivot point
and
is the moment of inertia of the body about the pivot point
and ![]() is the distance from the pivot to its center of mass.
is the distance from the pivot to its center of mass.
PROCEDURE: The ULI (Universal Lab Interface) should be connected to a sonic ranger that you will place on the floor looking up at a mass hanger. The mass hanger consists of two parts whose total mass must be included in your calculations. Don't forget this. Additional masses are placed on top of the hanger's tilted top side. The mass hanger is attached to a spring that is suspended from a stand. The stand must be securely clamped or screwed into the table top.
First, determine the spring constant, ![]() , using Eqn. (1) and
, using Eqn. (1) and ![]() .
Do this by measuring the CHANGE in the mass hanger's height for the
CHANGE in the added weight and determine
.
Do this by measuring the CHANGE in the mass hanger's height for the
CHANGE in the added weight and determine ![]() as outlined on the data
sheet. Use masses of 50, 100, 150, 200, and 250 g. For this part of
the lab, you do not need to include the weight of the holder or spring.
Use LoggerPro to measure the distance. Set the data rate to 40 Hz.
as outlined on the data
sheet. Use masses of 50, 100, 150, 200, and 250 g. For this part of
the lab, you do not need to include the weight of the holder or spring.
Use LoggerPro to measure the distance. Set the data rate to 40 Hz.
Now suspend a total mass of 200 g (including hanger) from the spring. Pull the hanger down by a small amount so that it oscillates with a full swing (i.e., twice the amplitude) of only 5 to 8 cm. That's enough to get good data. Make sure it is oscillating vertically and not rocking or swinging sideways.
WARNING: DO NOT DROP WEIGHTS ON THE SONIC RANGER BY CARELESSLY YANKING DOWN AND OVERDRIVING THE SPRING. THIS WILL MAKE THE WEIGHTS FALL OFF THE HANGER.
Collect data for about 10 seconds. LoggerPro should give you
a graph of ![]() versus time. If the x- and/or y-axis scales are too small
to clearly see the SHM, you will want to change the axes setting on the
graph to magnify it. Be sure that you can clearly see several whole
waves and use this to determine the period of oscillation. You may want to
use LoggerPro's Analyze feature. Attach a copy of the graph
to your report form.
versus time. If the x- and/or y-axis scales are too small
to clearly see the SHM, you will want to change the axes setting on the
graph to magnify it. Be sure that you can clearly see several whole
waves and use this to determine the period of oscillation. You may want to
use LoggerPro's Analyze feature. Attach a copy of the graph
to your report form.
Next you will examine the relationship between the displacement, velocity, and acceleration. Under Display select Two Graphs and set up separate displacement and velocity windows. The scale of the velocity graph may be too large to be useful, so rescale it in the same way as you did for the displacement graph. Also the horizontal x axis may too large. Change its span from 0 to 3 s for BOTH graphs.
Next, under Analyze select DATA A and you will get a screen with a large vertical bar that enables you to analyze the graphs. Notice that below the graphs there is a tabular readout of Time, Distance (Displacement), Velocity, and Acceleration. Ignore Force because its meaning is useless; we are not using a force probe. Note these values on the graphs as you move the cursor. You will use this table to analyze the sinusoidal graphs. After you have finished studying the displacement, velocity, and acceleration relationships, you will examine the dependence of the period on the amplitude and mass.
When you have finished the experiment go to File and select Quit. Select Don't Save to get rid of your data so that the disk doesn't get cluttered with old data.