Name:
Section:
Partner: Date:
PURPOSE: To explore the gravitational force and Kepler's Laws of Planetary motion.
INTRODUCTION: Newton's law of Universal Gravitation tells
us that the gravitational attraction between two masses, ![]() and
and ![]() , is
of magnitude
, is
of magnitude
| (1) |
where
![]() and
and ![]() is their
radial separation. In this experiment you will use the simulation
program Interactive Physics to investigate a number of the
consequences of this interaction. To make your calculations easier we
will invent a universe where gravity is not the weakest of forces, but
a very strong one; we will assume
is their
radial separation. In this experiment you will use the simulation
program Interactive Physics to investigate a number of the
consequences of this interaction. To make your calculations easier we
will invent a universe where gravity is not the weakest of forces, but
a very strong one; we will assume
![]() .
.
For this simulation you will need to know the potential energy, ![]() ,
of mass
,
of mass ![]() due to the gravitational attraction of
due to the gravitational attraction of ![]() ,
,
| (2) |
and the relationship between the speed of ![]() when in a
circular orbit about
when in a
circular orbit about ![]() and the distance
and the distance ![]() between
between ![]() and
and ![]() . This is derived from Newton's second law:
. This is derived from Newton's second law:
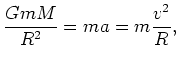 |
(3) | ||
| (4) |
From this equation you can easily relate the kinetic energy to ![]() .
.
SIMULATIONS: Impact: Open the Interactive
Physics simulation Escape, which shows the two masses ![]() and
and
![]() separated by a distance
separated by a distance ![]() . Note the anchor on
. Note the anchor on ![]() which means
it is pinned down and will not move during the simulation. Pull down
the Window menu and click on Properties. Record the
initial values below. To find
which means
it is pinned down and will not move during the simulation. Pull down
the Window menu and click on Properties. Record the
initial values below. To find ![]() pull down the World menu and
click on Gravity.
pull down the World menu and
click on Gravity.
![]() :
: ![]() :
: ![]() :
: ![]() :
:
![]() :
: ![]() :
: ![]() :
:
Calculate (predict) the initial potential
energy: . (Show your work.) At what
value of ![]() is this energy equal to zero?
is this energy equal to zero?
Is this the potential energy of ![]() or is it the potential energy of
the entire system? Why?
or is it the potential energy of
the entire system? Why?
Run the simulation, record the K.E. and P.E. and calculate the total
energy. [Note that P.E. in the simulations may incorrectly hace units of
kg![]() /m instead of joules. It does correctly calculate the value.]
/m instead of joules. It does correctly calculate the value.]
What can you conclude about the total energy during the fall? What about after the impact?
Next predict the velocity ![]() ,
called the escape velocity, that it is necessary for
,
called the escape velocity, that it is necessary for ![]() to have in
order for it to move infinitely far away from
to have in
order for it to move infinitely far away from ![]() . (Show your work.)
. (Show your work.)
![]() =
=
Click on ![]() and enter the escape velocity plus 1 m/s into the Properties box for
and enter the escape velocity plus 1 m/s into the Properties box for ![]() of Body[3]. Before you run the simulation
reduce the size of the image. Pull down the View menu, then
select View Size. Set the window width to 40 m. You may also
choose the negative looking glass (negative zoom) from the tool box
and click the screen several times to reduce the scale of the
image. Use the scroll bars to reposition the reduced image to a
convenient location. Run the simulation and record the K.E. and
P.E. in the table below and calculate the total energy. What can you
conclude about the total energy during the flight?
of Body[3]. Before you run the simulation
reduce the size of the image. Pull down the View menu, then
select View Size. Set the window width to 40 m. You may also
choose the negative looking glass (negative zoom) from the tool box
and click the screen several times to reduce the scale of the
image. Use the scroll bars to reposition the reduced image to a
convenient location. Run the simulation and record the K.E. and
P.E. in the table below and calculate the total energy. What can you
conclude about the total energy during the flight?
Circular Orbits: Now predict the velocity ![]() you will need to
give
you will need to
give ![]() in order to put it into a circular orbit around
in order to put it into a circular orbit around ![]() . Click
on
. Click
on ![]() and enter this value for
and enter this value for ![]() into the Properties box
for Body[3]. Reset
into the Properties box
for Body[3]. Reset ![]() to 0. Adjust the window width to 15 m so
that you will be able to see all (or most ) of the orbit. Click on
to 0. Adjust the window width to 15 m so
that you will be able to see all (or most ) of the orbit. Click on ![]() ,
pull down the Define menu and click on velocity and acceleration
to add these vectors to your simulation. Under World select
Tracking and choose every 16 frames. Run the simulation.
,
pull down the Define menu and click on velocity and acceleration
to add these vectors to your simulation. Under World select
Tracking and choose every 16 frames. Run the simulation.
![]() Describe how the angle between the velocity and
acceleration vectors changes with time and how this is related to the
fact that both potential and kinetic energy remain constant. [Answer
this in the typewritten report]
Describe how the angle between the velocity and
acceleration vectors changes with time and how this is related to the
fact that both potential and kinetic energy remain constant. [Answer
this in the typewritten report]
You may want to rescale your graphs to make the curves more visible. To do this, pull down the Window menu, choose Appearance, and click on each graph in turn. To rescale, type in new values for the min or max of the x (time) and y axes in the appearance box.
Kepler's First Law: All planets move in elliptical orbits with
the Sun (![]() ) at one focus. Open the simulation Orbit. This
is almost the same simulation as Escape except some default
settings are different. First set the initial value of
) at one focus. Open the simulation Orbit. This
is almost the same simulation as Escape except some default
settings are different. First set the initial value of ![]() equal to
the value you calculated for a circular orbit and run the simulation
to confirm your result. Now set
equal to
the value you calculated for a circular orbit and run the simulation
to confirm your result. Now set ![]() to 25 m/s and then 15 m/s (you
may want to change the number of frames tracked or time increment).
Run the simulation and determine the distances of apocenter (furthest
recession)
to 25 m/s and then 15 m/s (you
may want to change the number of frames tracked or time increment).
Run the simulation and determine the distances of apocenter (furthest
recession) ![]() , pericenter (closest approach)
, pericenter (closest approach) ![]() (the
corresponding terms for motion around the sun are aphelion and
perihelion and for motion about the earth, perigee and apogee). Note
that
(the
corresponding terms for motion around the sun are aphelion and
perihelion and for motion about the earth, perigee and apogee). Note
that ![]() and
and ![]() are magnitudes (i.e., always positive).
are magnitudes (i.e., always positive).
![]() :
: ![]() :
: ![]() :
:
![]() : 25
: 25 ![]() :
: ![]() :
:
![]() : 15
: 15 ![]() :
: ![]() :
:
The equation for an ellipse is given by
![]() . Find
. Find ![]() and
and ![]() in terms of
in terms of ![]() and
and ![]() .
.
![]() Describe how the angle between the velocity and
acceleration vectors changes with time. Explain why and how it
differs from the case of a circular orbit and how the change in
kinetic and potential energy is related to the angle. Attach plots
showing how the velocity and acceleration vectors change throughout
the orbit. [Answer this in your typewritten report].
Describe how the angle between the velocity and
acceleration vectors changes with time. Explain why and how it
differs from the case of a circular orbit and how the change in
kinetic and potential energy is related to the angle. Attach plots
showing how the velocity and acceleration vectors change throughout
the orbit. [Answer this in your typewritten report].
Kepler's Third Law: The square of the period of a planet is
proportional to the cube of the semi-major axis of the orbit -
![]() . Run the simulation for various
values of
. Run the simulation for various
values of ![]() and measure the period
and measure the period ![]() ,
, ![]() , and
, and ![]() . For each
orbit calculate
. For each
orbit calculate ![]() and compare with the predicted value. For 28
m/s you may want to increase the step size of the calculation to 0.2 s.
and compare with the predicted value. For 28
m/s you may want to increase the step size of the calculation to 0.2 s.
Detecting Planets: The gravitational force acts equally strongly
on both bodies. So in our previous simulations the motion of ![]() is
affected by the pull of
is
affected by the pull of ![]() , but we didn't notice this because we
anchored
, but we didn't notice this because we
anchored ![]() to the computer screen. Open the simulation Binary. Notice that the anchor on
to the computer screen. Open the simulation Binary. Notice that the anchor on ![]() has been removed and its mass has
been reduced. Calculate the velocity
has been removed and its mass has
been reduced. Calculate the velocity ![]() that
that ![]() needs to order to
have a circular orbit, using equation (4). Put this value into the
Properties chart for
needs to order to
have a circular orbit, using equation (4). Put this value into the
Properties chart for ![]() and run the simulation. Explain why
and run the simulation. Explain why ![]() moves to the right across the screen even through
moves to the right across the screen even through ![]() was zero for
it. Within roughly the past 5 years nearly 100 large planets have been
discovered around nearby stars by observing the star's motion under
very high resolution conditions.
was zero for
it. Within roughly the past 5 years nearly 100 large planets have been
discovered around nearby stars by observing the star's motion under
very high resolution conditions.
Make appropriate changes in the initial parameters for ![]() and
and ![]() so
that the drift in
so
that the drift in ![]() does not appear. Do not change the masses!
Print a copy of the simulation for your lab report showing that you
successfully stopped the drift.
does not appear. Do not change the masses!
Print a copy of the simulation for your lab report showing that you
successfully stopped the drift.
Three-Body Gravitational Problems
The solution for the two body gravitational problem has a simple analytical solution of one of the conic sections, i.e., the motion is always a circle, ellipse, parabola, or hyperbola. You might think that adding a third body would make the problem just a little more complicated. In fact, it makes it impossible to solve analytically! Even worse, the system becomes chaotic. Chaotic means that the system is so sensitive to the initial conditions that we cannot predict the long term behavior. A very small change in the starting position or velocity will make a very big change later on. The addition of a third body can also give some very interesting effects.
I. First open the file 3-body. This has a system set up with a heavy mass (50,000 kg - the middle mass), a medium mass (500 kg, the bottom one) and a light mass (1 kg, the top one). This represents a planetary system with a star, large planet, and small planet. Run the simulation. Notice how quickly the orbit of the small planet is perturbed. Although it begins in a nearly circular orbit, it is soon forced into a very eccentric elliptical orbit. The small planet has received a boost from the larger planet. The phenomenon is used to give a space probe much larger velocities than can easily be achieved from a rocket.
II. Let's look at the boost phenomenon a little
more carefully. Open file 3-body-boost. This represents the
case of a probe being launched from an orbit close to the sun and
using a large planet far from the sun to get a boost. Look carefully
to what happens as the probe goes by the planet. Display the
acceleration and velocity of body 2 and step through the simulation.
Where does the probe get its extra energy? If you change body-1's
velocity from ![]() 0.5 to 0 and body-3's mass to 1 kg, you can see what
the path would have been without the effect of a large planet.
0.5 to 0 and body-3's mass to 1 kg, you can see what
the path would have been without the effect of a large planet.
Just such a boost was used by Voyager 2 (from NASA, not Star Trek). Voyager was launched in 1977 and passed Jupiter, Saturn, Uranus, and Neptune (in 1989), using each successive planet to boost itself to the next one. Such a ``Grand Tour'' (as it was called) is possible only if the planets are properly aligned, something which occurs only once every 175 years. Calculate how long it would take the probe to get to Neptune if it were put in an elliptical orbit with perihelion equal to the Earth's radius and aphelion equal to Neptune's radius, and compare to the 12 years it actually took.
Finally, to see an example of sensitivity to initial conditions,
change the probe's initial velocity ![]() from
from ![]() to
to ![]() (leaving
(leaving ![]() unchanged). Compare with the previous track to see how
a very small change in the velocity changes the path completely.
Watch the simulation for about 750 time units. This gives a very nice
example of a triple boost. Show that after the final boost the probe
will escape the system. Changing the initial velocity to
unchanged). Compare with the previous track to see how
a very small change in the velocity changes the path completely.
Watch the simulation for about 750 time units. This gives a very nice
example of a triple boost. Show that after the final boost the probe
will escape the system. Changing the initial velocity to ![]() also gives an interesting path.
also gives an interesting path.
LAB REPORT
Please hand in the lab next week. Your report should consist of this
write-up with the original data and questions answered. You should
have a copy of the simulation showing the orbiting planet after you've
adjusted the motion of the star to make the system stationary.
Explain and show the calculations of how you determined this. In
addition, give a typewritten response to the questions on pages 3 and
4 (the ones marked with
![]() ). You may combine the
answers into one general explanation if you feel it makes the
explanation clearer.
). You may combine the
answers into one general explanation if you feel it makes the
explanation clearer.