Name: Section:
In the ballistic pendulum experiment the prediction of the range
depended on the height the pendulum arm swung up and the height of the
chair. Equation (8) of your write-up states that the range, ![]() . is
given by
. is
given by
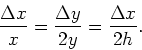
Let ![]() m,
m,
![]() m,
m, ![]() m,
m,
![]() m,
m, ![]() g and
g and ![]() g. What is the relative uncertainty in
g. What is the relative uncertainty in ![]() and
and ![]() ? Set
? Set ![]() to 0.09, change
to 0.09, change ![]() by 0.01 and find the change in
the range. Then keep
by 0.01 and find the change in
the range. Then keep ![]() set to 0.55 and change
set to 0.55 and change ![]() by 0.002 and find
the change in range. In each case compare the change to
by 0.002 and find
the change in range. In each case compare the change to ![]() and
and ![]() . Comment on the contribution to the uncertainty of
the range by each variable and why
. Comment on the contribution to the uncertainty of
the range by each variable and why ![]() has a larger absolute
uncertainty but smaller contribution to the uncertainty of
has a larger absolute
uncertainty but smaller contribution to the uncertainty of ![]() .
.