X-Ray Powder Diffraction

X-RAY ANALYSIS OF A SOLID

Experiment Developed with National Science Foundation Funding.

Learning Experiences

- Use of the Bragg Equation
- Modern Chemical Analysis
- Fingerprinting a Solid
- Computer Graphics

Pre-Lab Question

1. List all safety precautions that must be observed in the use of x-rays.

X-Ray Diffraction Experiment

INTRODUCTION

X-rays are electromagnetic radiation of wavelength about 1 Å (10-10 m), which is about the same size as an atom. They occur in that portion of the electromagnetic spectrum between gamma-rays and the ultraviolet. The discovery of X-rays in 1895 enabled scientists to probe crystalline structure at the atomic level. X-ray diffraction has been in use in two main areas, for the fingerprint characterization of crystalline materials and the determination of their structure. Each crystalline solid has its unique characteristic X-ray powder pattern which may be used as a "fingerprint" for its identification. Once the material has been identified, X-ray crystallography may be used to determine its structure, i.e. how the atoms pack together in the crystalline state and what the interatomic distance and angle are etc. X-ray diffraction is one of the most important characterization tools used in solid state chemistry amd materials science.
We can determine the size and the shape of the unit cell for any compound most easily using the diffraction of x-rays.

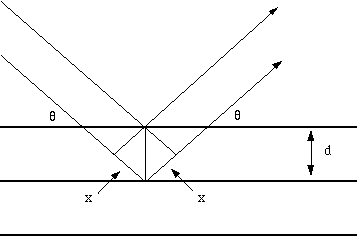
Fig. 1 Reflection of x-rays from two planes of atoms in a solid.

The path difference between two waves:

2 x wavelength= 2dsin(theta)

For constructive interference between these waves, the path difference must be an integral number of wavelengths:

n x wavelength= 2x

This leads to the Bragg equation:

n x wavelength = 2dsin(theta)

Figure 2 shows the x-ray diffraction pattern from a single crystal of a layered clay. Strong intensities can be seen for a number of values of n; from each of these lines we can calculate the value of d, the interplanar spacing between the atoms in the crystal.

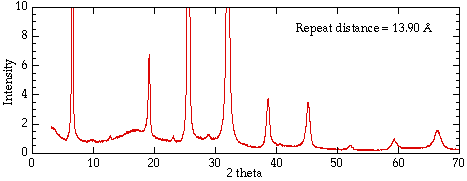
Fig. 2 X-ray diffraction pattern from a layered structure vermiculite clay.

EXAMPLE 1 Unit Cell Size from Diffraction Data

The diffraction pattern of copper metal was measured with x-ray radiation of wavelength of 1.315Å. The first order Bragg diffraction peak was found at an angle 2theta of 50.5 degrees. Calculate the spacing between the diffracting planes in the copper metal.

The Bragg equation is

n x wavelength = 2dsin(theta)

We can rearrange this equation for the unknown spacing d:

d = n x wavelength/2sin(theta).

theta is 25.25 degrees, n =1, and wavelength = 1.315Å, and therefore

d= 1 x 1.315/(2 x 0.4266) = 1.541 Å

In this lab you will measure the x-ray powder diffraction pattern from a single crystal. Your TA will give you the sample to be measured and show you how to set up the Miniflex x-ray diffractometer.

You should measure all the values of 2theta from the chart, and after converting them into d values calculate the repeat distance in your unit cell. In your lab note book list all the 2theta values with their corresponding values of n and d. Then calculate the mean and median values of the unit cell.

INSTRUMENTATION

The X-ray diffraction experiment requires an X-ray source, the sample under investigation and a detector to pick up the diffracted X-rays. Fig 3 is a schematic diagram of a powder X-ray diffractometer.

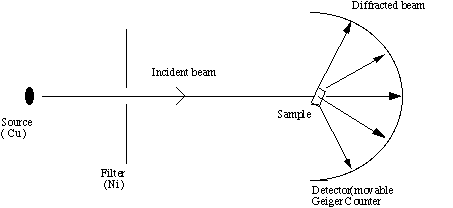
Fig. 3. Schematic of an X-ray powder diffractometer

The X-ray radiation most commonly used is that emitted by copper, whose characteristic wavelength for the K radiation is =1.5418Å. When the incident beam strikes a powder sample, diffraction occurs in every possible orientation of 2theta. The diffracted beam may be detected by using a moveable detector such as a Geiger counter, which is connected to a chart recorder. In normal use, the counter is set to scan over a range of 2theta values at a constant angular velocity. Routinely, a 2theta range of 5 to 70 degrees is sufficient to cover the most useful part of the powder pattern. The scanning speed of the counter is usually 2theta of 2degrees min-1 and therefore, about 30 minutes are needed to obtain a trace.

PROCEDURE

**Do not open the chamber while the alarm red light is on
**Never touch the detector (may result in signal off).

Obtain a sample from your instructor, place it onto the double-side tape which is then placed on an aluminum sample holder; if you are preparing a powder sample, use a spatula to spread the powder onto the double-side tape.
Read the instructions for the Miniflex X-ray diffractometer, which are on the wall above the instrument. Your instructor will explain the operation.
Set the instrument at optimum setting as follows
time constant 2
range ?
chart speed: Low
Slide in the sample holder and adjust the beginning 2theta at 70 degree (It scans from high degrees to low degrees)
Switch on the start knob and chart recorder (slow) simultaneously, run your sample on slow chart speed.
Once scan gets down to 3 degree of 2theta , stop (switch start knob to off) and chart. TURN OFF X-ray.
Locate all peaks on the chart and corresponding 2theta values and write their values into the data chart below. Perform the necessary calculations in the table and calculate the repeat distance in your unit cell.

Data Table of X-ray Diffraction Peaks
2theta theta sin(theta) n d=n x wavelength/sin(theta) lattice spacing
= n x d

1

2

3

4

5

6

7

8

Wavelength = 1.5418 Å for Cu Ka

For more information please contact Stan Whittingham: stanwhit@binghamton.edu