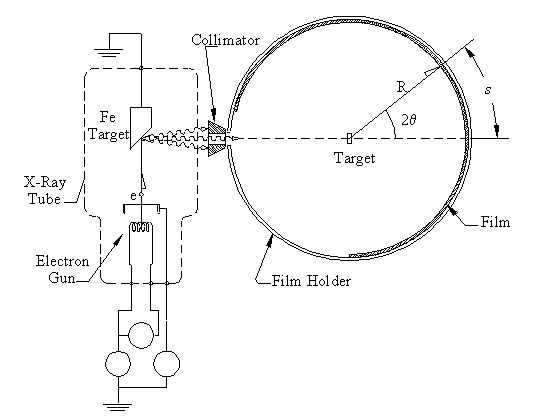
Figure 6: X-ray diffraction set-up. X-rays are produced in an x-ray
tube that are collimated onto the sample. A cylindrical film records
where the x-rays strike.
Due to safety reasons you will not be able to perform an x-ray diffraction experiment. Instead you do a simulated experiment that demonstrates how crystallography is actually done.
X-rays are produced by accelerating electrons through a potential difference, usually several tens of thousands of volts. The electrons strike a target, and some of their kinetic energy is converted into x-ray radiation as they are decelerated (see Fig. 6). The x-rays are collimated and then strike the target. In a powder diffractometer a piece of photographic film is mounted on a cylindrical holder. When an x-ray is diffracted through an angle 2θ, it strikes the film at an arc distance s along the film. The film is developed an a series of lines can be measured where the separation between lines is related to 2θ.

Figure 6: X-ray diffraction set-up. X-rays are produced in an x-ray
tube that are collimated onto the sample. A cylindrical film records
where the x-rays strike.
The most energetic photons produced in the tube by electron bombardment of the Fe target are from a sort of inverse photoelectric effect in which all the kinetic energy (eV) of one electron is given to one photon: hf = eV. This limiting process sets the short wavelength limit of the x-ray spectrum. However, the most intense x-ray radiation emitted from the target is due to excitation of target atoms by the impinging energetic electrons followed by de-excitation of the atoms with emission of x-rays characteristic of the atomic levels in the target material. The Kα x-rays are in fact two photons closely spaced in energy produced by transitions of electrons in the target from the LII and LIII levels to a vacancy created in the K shell. The Kβ x-rays are due to transitions of electrons from certain M shell levels to a vacancy in the K shell. (Some transitions are forbidden by selection rules; e.g., LI to K shell transitions do not occur.) The binding energies for an Fe atom are listed in Table 1.
| Shell | Energy (eV) |
| K | 7112 |
| LI | 842 |
| LII | 721 |
| LIII | 709 |
| M | 50 |
General notes
Any x-ray diffraction experiment shows both the particle and wave
nature of x-rays. The crystal diffraction displays the wave nature of
x-rays, while the x-ray spectrum emitted from the target displays the
particle or "photon" nature of x-rays. The target is bombarded with
energetic electrons comprises a "characteristic" spectrum, specific to
the target material, and a "continuous" spectrum. The latter has a well
defined short wavelength limit, which depends on the maximum energy of
the electron beam that impinges on the target; i.e., the limit depends
on the accelerating voltage applied to the x-ray tube. In your
discussion in your lab report, you should comment on this. As discussed
below you will relate the lines that appear in the characteristic
spectrum to energy levels in the target atom, but you should also
answer the following question: What is the minimum accelerating voltage
that must be applied to an x-ray tube in order to produce the K series
x-rays? State the numerical value for the case of an iron target - our
case. Also, the measurement of the short wavelength limit of the
continuous spectrum provides a good method for determination of h/e.
Explain how this is done in terms of the photon nature of radiation.
Your discussion should also address the phenomenon of "absorption
edges" in the x-ray absorption spectrum by relating the adsorption
spectrum to the atomic energy level diagram.
Experiment
Examine the x-ray apparatus and prepare a
rough sketch that depicts a powder crystal diffraction experiment. The
sketch should show: electron path in x-ray tube, x-ray tube target,
x-rays going from target into powder crystal camera, slits that define
x-ray beam going to sample under study, sample, beam catcher for
directly transmitted beam, diffracted x-ray beam, film strip. The x-ray
film strip is bent into a circle of radius R. Dissemble the powder
crystal camera (if it is not already done) enough so that you can
measure R, and indicate the value for R on your sketch.
Sometime in the past a diffraction pattern was taken for a NaCl powder using an Fe target in the x-ray tube. The line pattern from the film is reproduced in Figure 7 at the end of this write-up (the actual film is displayed in the lab). NaCl has a cubic crystal structure with a lattice constant of 5.64 Å. The distance d1 in Fig. 3b is 2.82 Å (one-half of the lattice constant because there are two kinds of atoms in the crystal). The straight through beam with 2θ = 0 is marked on the drawing. In addition one line on the film has been indexed with the value of n, the x-ray wavelength, Kα, and the d spacing that give rise to this line. The distance s from the direct beam is given as well. The distances s for the other five lines can be scaled from the drawing. (The distance that is given may not measure quite the quoted value even though the drawing was made to scale; the Xerox machine does not reproduce quite 1:1; thus, all distances should be scaled to the indexed distance given.)
Index the remaining 5 lines on the film using Bragg's Law, Eq. 2. You will do this by giving the d spacing, n, and x-ray wavelength (in terms of the transition name). To do this you need to first calculate the wavelengths of the different transitions from the binding energies in Table 1. The Kα wavelength you should use is the average of the two different Kα transitions. To help you do this you should fill in the appropriate values for λ, θ, and s in Table 2. The value you compute for s and the value of s measured on the film should be close; you can use this as a check for goofs in setting up your calculations. Identify each line on the drawing of the observed spectrum and show the identification on the drawing (i.e., show whether planes d1 or d2, the n value, and whether the line is due to the Kα or the Kβ x-rays.). Include the film in your lab report.
| Lattice plane (Å) | n | X-ray λ | λ (Å) | θ | s(cm) | |
| d1 | 2.82 | 1 | Kα | |||
| d1 | 2 | Kα | ||||
| d2 | 1 | Kα | ||||
| d2 | 2 | Kα | ||||
| d1 | 1 | Kβ | ||||
| d2 | 1 | Kβ | ||||
Prepare a similar table for a graphite (carbon) target like the one you used in the electron diffraction experiment. The plane distances d1 and d2 will be those found in that experiment, and the relation of d1 to d2 should be appropriate to the hexagonal structure. Assume that you would be using the same iron x-ray tube target that produced the NaCl data. Locate, identify and draw all the possible lines that should appear on an x-ray film. Use the blank film to the right of the NaCl drawing to make your sketch of the graphite diffraction pattern. Use the same scale as the NaCl film so the two drawings will look like two films placed side by side. In your lab report explain by analysis how an unknown crystal structure could be determined from a powder diffraction experiment.
In addition to electrons and x-rays, neutrons are also used to study the structure of materials by diffraction experiments. In order to better appreciate the energy ranges and appropriate wavelengths of the different radiation, complete Table 3 and place it in your lab report.
| Radiation | Velocity [m/s] |
Wavelength [Å] |
| 6400 eV x-rays | ||
| 34,000 eV x-rays | ||
| 1500 eV electrons | ||
| 5000 eV electrons | ||
| 0.025 eV neutrons | ||
| 1500 eV neutrons |
The following comments may help interpret the significance of the entries in the table. The characteristic iron x-rays are about 6400 volts (i.e., photon energy is 6400 eV). The diffraction experiment that gave the NaCl pattern of the attached drawing was run with a peak voltage of about 34,000 volts; hence, the short wavelength limit of the x-ray spectrum produced in that case corresponds to the 34,000 volt x-ray entry in Table 3. The voltages shown for electrons span those used in our electron diffraction experiment. The entries for neutrons indicate the very low energy neutrons must have in order to get wavelengths of the order of inter-atomic dimensions. Thermal neutrons (i.e., neutrons in thermal equilibrium with their surroundings) from a nuclear reactor are usually used for neutron diffraction studies.
Discuss the different sorts of information that may be elicited by electron, x-ray, and neutron diffraction studies. To a considerable extent these different kinds of studies are complementary, which should be emphasized in your discussion. You may need to talk to your instructor and do a little reading to answer these questions.
Finally, the phenomena demonstrated in all three parts of this laboratory played important roles in the early development of quantum theory. Your introduction in your lab report should include some account of this history.
This figure should be completed and included in the write-up. It is available as an Adobe PDF file, a GIF file, or as an AutoCAD DWG file.
 | School of Physics at Georgia Tech |