10/7/13

Introduction to Many Body Physics.

620 Fall 2026

Piers Coleman, Rutgers University.
First class 3.50pm 11th Sept.
Images Monograph Texts
 Exercises
 Times of Course
 Syllabus outline
 Timetable
 



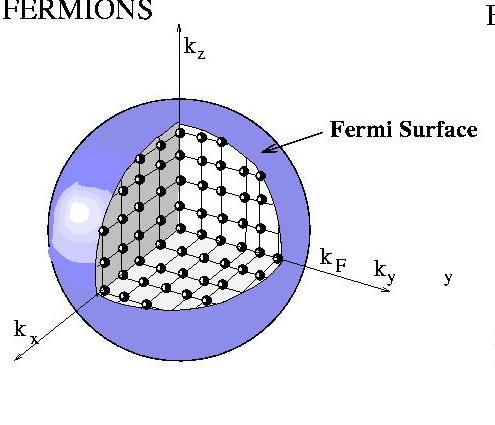
Maxwellian construction of a Fermi Surface
Cuprate superconductor levitating a magnet.



Quantum Critical Point:
"Black hole" in the material phase diagram.


Adiabatic concept: basis of perturbation theory.

(Return to top)


Instructor: Piers Coleman, Room 268
If you have any enquiries about this course or the homework, please do not hesitate to contact me via email at : coleman@physics.rutgers.edu

Scope of Course. Many body physics provides the framework for understanding the collective behavior of vast assemblies of interacting particles. This course provides an introduction to this field, introducing you to the main techniques and concepts, aiming to give you first-hand experience in calculations and problem solving using these methods.

Students with disabilities 
 





    Introduction to Many Body Physics.

          The content of this course, with additional material will be my book "Introduction to Many Body Physics", published by Cambridge University Press and available as the adopted course book at the Rutgers Bookstore and also at Amazon. 

Introduction to Many Body Physics.


 
(Return to top)



  • Texts: Here are some other excellent references for the course.
      •  

      • Many-Particle Physics, Third Edition  by G. Mahan. (Plenum, 2000). A classic text on Many body physics.  Focuses on diagramatic and Greens Functions method. Very thorough but a little  dated.
      • Condensed Matter Field Theory by Alexander Altland and Ben Simons.(CUP, 2006)
        An excellent introduction to Field Theory applied in condensed matter physics. I almost decided to make this the main text, as I like it greatly. 
      • Basic Notions in Condensed Matter Physics by P. W. Anderson. A classic reference. Many of us still turn to this book for inspiration, and philosophy. It also has a fine selection of important reprints at the back.


      Traditional Many Body Theory and Greens Functions
       

      • ``Methods of Quantum Field Theory in Statistical Physics'' by Abrikosov, Gorkov and Dzyalozinskii. (Dover Paperback) - Classic text from the sixties, known usually as AGD.
      • ``A guide to Feynman Diagrams in the Many-Body problem by R. D. Mattuck. A light introduction to the subject. Reprinted by Dover.
      • ``Greens functions for Solid State Physics'' S.Doniach and E. H. Sondheimer. Not as thorough as AGD, but less threatening and somehow more manageable. Frontiers in Physics series no 44.
      • ``Quantum Many Particle Systems'' by J. W. Negele and H. Orland. Alas all the good physics is in the unsolved excercises! However, it is the only one of this set to touch on the subject of functional integrals.


      Newer approaches to Many-Body Problem.
       

      • R. Shankar, Rev Mod Phys 66 129 (1994). An amazingly self-contained review of the renormalization group and functional integral techniques written by one of the best expositors of condensed matter physics.
      • ``Field Theories of Condensed Matter Physics'' by E. Fradkin. (Frontiers in Physics, Addison Wesley). Interesting material on the fractional statistics and the fractional quantum Hall effect.
      • ``Quantum Field Theory in Condensed Matter Physics'' by A. Tsvelik. (Cambridge paper back) Very good for one dimensional systems. No exercises.


      Further references:

      • The Theory of Quantum Liquids by D. Pines and P. Nozieres. Excellent introduction to Fermi liquid theory that avoids the use of field theory.
      • Statistical Physics, vol II by Lifshitz and Pitaevskii. Pergammon. Marvellous book on applications of many body physics, mainly to condensed matter physics.

      Online references     (Check it out- this is a great link).

(Return to top)



Exercises 620 (Return to top)

          Initial quiz       
        
          Homework 1
   
(Return to top)        Note: this material is copywritten and should not be posted without permission.
 
10.20-11.40am on  Wednesday  and 3.50-5.10 on Friday in  Serin 287E  on Busch campus. Occasionally, to make up for my travel, we will hold an additional  class at 2pm on Mondays in Serin 287E. I apologize for this inconvenience.

Office hour:   9:50am Tuesday or by arrangement.  Tel x 9033

Assessment:   Assessment will be made on the basis of weekly assignments, a take-home mid-term and a take-home final exam. I want to encourage an interactive class and will take this into account when grading!

(Return to top)



Outline  We will make a selected sortie through the following list. Asterisks indicate areas that will be high priority

  • Second Quantization. ``Free'' systems-- the building block of the quasiparticle concept. *
  • Phonons and photons, Fermi and Bose fluids; spin-systems (x-y) model. Interactions.*
  • Green's Functions and Feynman diagrams .*
  • Finite temperature Green Functions.  *
  • Application of Finite temperature  Feynman Diagrams to (i) electron-phonon problem * ; (ii) transport theory.
  • Functional Integral Approach (if time permits).
  • Broken Symmetry and Superconductivity.  *



(Return to top)

         Schedule (Evolving schedule. First class to start 11th Sept in Fall 2026) :

Week

 Monday Make-up
2pm Serin 287E
 Weds 10:20
Serin 287E 		Friday 3:50pm
Serin 287E
0. Aug 31-Sep 4

On travel
 On travel

1. Sept 7-11
On travel
 First Class:
Fields overview.
Einsteins phonon: the Harmonic Oscillator

2 Sept 14-18
Collective Quantum Fields: 1 and 3D Collective Quantum Fields: continuum and thermodynamic limit.

3 Sept 21-Sept 25
 Conserved Particles:
Canonical Commutation Rules

Jordan_Klein_2027.pdf
 Interactions Particles in thermal equilibrium.
4 Sept 28-Oct 2
 Examples of 2nd Quantization
1 D Antiferromagnet. Hubbard Model
Examples of 2nd Quantization
Jordan Wigner Transformation, 1D Ferromagnet.		 Examples of 2nd Quantization
Free Bosons, Fermions

5 Oct 5-  Oct 9
 Examples of 2nd Quantization: Boltzmann Density Matrix Greens Functions:
Generating function for bosons 		Greens Functions:
Free Fermions and Bosons

6. Oct 12- Oct 16
 Generating function for Fermions. Spectral decomposition. No Class: on Travel No Class: on Travel

7. Oct  19 - Oct 23
 Adiabaticity
Gell-Mann Low  		Landau Fermi
Liquid Theory		 T=0
Feynman Rules
Heuristic Derivation

8. Oct 26-  Oct 30
T=0
Feynman Rules
Linked Cluster Theorem		 T=0
Electron in scattering potential. Hartree Fock.

9.  Nov  2- Nov 6
 More Mr Feynman Response functions. Lindhard Function. No Class: on Travel

10.  Nov 9- Nov 13
 RPA Approach.
Large N electron gas 		Finite T
Imaginary time
Greens functions		 Finite T
Feynman Rules and examples

11.  Nov 16 - Nov 20
 (On Travel)
 No Class On Travel
 Finite T:
Electron Phonon
interaction: self energy; Migdal's theorem.

12.  Nov 23 -Nov 27
  Superconductivity   Preliminaries For discussion. Since this is a Rutgers rescheduled Friday and our class would be at 3.40pm. Probably cancelled as people travelling.
No Class: Thanksgiving

13.  Nov 30 - Dec 4
Superconductivity   BCS Theory I  Superconductivity BCS Theory II


 Superconductivity BCS III

14.  Dec 7 -  Dec 11
 (On Travel)
 No Class on Travel
 No Class: End of Semester.


(Return to top)