


Physics 418, Homework Assignment
Due in Class, Wednesday, February 4, 2004
- Isaac Asimov in his novel The Gods Themselves describes a
universe where the most stable nuclide with A=186 is not
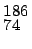 W but rather
W but rather 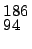 Pu. This is claimed to be
a consequence of the ratio of the strengths of the strong and
electromagnetic interactions being different from that in our
universe. Assume that only the electromagnetic coupling constant,
Pu. This is claimed to be
a consequence of the ratio of the strengths of the strong and
electromagnetic interactions being different from that in our
universe. Assume that only the electromagnetic coupling constant,
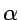 , differs and that both the strong interaction and the nucleon
masses are unchanged. How large must
, differs and that both the strong interaction and the nucleon
masses are unchanged. How large must 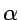 be in order that
be in order that
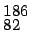 Pu,
Pu, 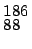 Pu and
Pu and 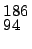 Pu are stable?
Pu are stable?
- In the Liquid Drop Model, the binding energy for nuclei is:
The Coulomb term in the semi-empirical mass formula
(aka. liquid drop model) is
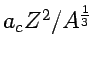 .
Try to estimate the value of
.
Try to estimate the value of 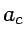 with
simple electrostatics.
First, show that the potential energy due to electrostatic
forces on a uniformly charged shpere of total charge
with
simple electrostatics.
First, show that the potential energy due to electrostatic
forces on a uniformly charged shpere of total charge 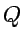 and
radius
and
radius 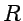 is
is
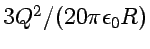 .
Estimate
.
Estimate 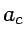 by using
by using
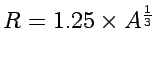 ,
the values for
,
the values for 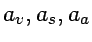 given in lecture, and the
binding energy (not mass!) of
given in lecture, and the
binding energy (not mass!) of
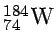 .
For the binding energy, use the value given in:
http://atom.kaeri.re.kr/ton/.
.
For the binding energy, use the value given in:
http://atom.kaeri.re.kr/ton/.
- The
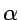 -decay of a
-decay of a 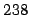 Pu (
Pu (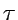 = 127 years) nuclide
into a long-lived
= 127 years) nuclide
into a long-lived 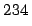 U (
U (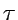 = 3.5 x 10
= 3.5 x 10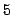 years)
daughter nucleus releases 5.49 MeV kinetic energy.
The heat so produced can be converted into useful electricity by
radio-thermal generators (RTG's).
The Voyager 2 space probe, launched 20-Aug-1977,
flew past four planets, including Saturn, which it reached
on 26-Aug-1981. Saturn's separation from the Sun is
9.5 AU (1 AU = Earth-Sun distance).
years)
daughter nucleus releases 5.49 MeV kinetic energy.
The heat so produced can be converted into useful electricity by
radio-thermal generators (RTG's).
The Voyager 2 space probe, launched 20-Aug-1977,
flew past four planets, including Saturn, which it reached
on 26-Aug-1981. Saturn's separation from the Sun is
9.5 AU (1 AU = Earth-Sun distance).
- How much plutonium would an RTG on Voyager 2 have to
carry in order to deliver at least 400 W electrical
power when the probe flies past Saturn? Assume
a power conversion efficiency of 6.2%.
- How much electric power would then be available
at Neptune, 30.1 AU from the Sun, on 24-Aug-1989?
- For comparison: the largest-ever ``solar paddles''
used in the space laboratory Skylab would have
produced 10.5 kW from an area of 730 m
 , 1 AU
from the Sun. What area of solar cells would
Voyager 2 have needed if those were its
power source?
, 1 AU
from the Sun. What area of solar cells would
Voyager 2 have needed if those were its
power source?
- Griffiths: Problem 1-3.
- Fraunhofer diffraction by a circular disk with diameter D
produces a ring-shaped diffraction pattern with the first
minimun at an angle
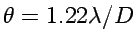 .
Calculate the angular separation of the diffraction minima
of
.
Calculate the angular separation of the diffraction minima
of 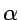 particles with energy E
particles with energy E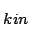 = 130 MeV
scattered of a
= 130 MeV
scattered of a 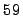 Co nucleus. The nucleus should be
considered as an impenetrable disk.
Co nucleus. The nucleus should be
considered as an impenetrable disk.



Thomas J. &
2004-01-28
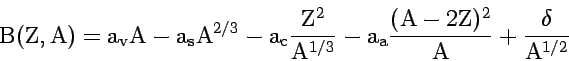
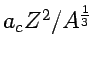 .
Try to estimate the value of
.
Try to estimate the value of 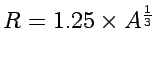 ,
the values for
,
the values for  , 1 AU
from the Sun. What area of solar cells would
Voyager 2 have needed if those were its
power source?
, 1 AU
from the Sun. What area of solar cells would
Voyager 2 have needed if those were its
power source?