For well over 50 years astrophysicists have been struggling with the
apparent mass discrepancies that seem to exist in large scale structures
throughout the universe (Zwicky 1937). The discovery of asymptotically
flat galactic rotation curves at large distances from the core (Bosma 1978) started an
avalanche of ``dark" matter (DM) ideas in an effort to explain the growing body of data. Interestingly, it seems that many current
versions of DM run into serious difficulties when compared with observed
properties of galaxies (Sellwood 2000). Moreover, with the discovery of the
likelihood of a global acceleration to the Hubble flow (Perlmutter et al. 1999;
Riess et al. 1998), it would seem that the time is ripe for a fundamentally
new approach, one which might have the possibility of explaining many
disparate observational problems. To this end, we postulate an additional mode for gravitational interaction in which the
field associated with a hypothetical particle is everywhere repelling. For simplicity,
we call the mass associated with this field ![]() , to distinguish it from
``ordinary"
matter, M. If the repelling field is inverse-square in nature, the combined gravitational and anti-gravitational force between
the M and
, to distinguish it from
``ordinary"
matter, M. If the repelling field is inverse-square in nature, the combined gravitational and anti-gravitational force between
the M and
![]() will be independent of separation, and thus
merely implies a change in the magnitude of G.
will be independent of separation, and thus
merely implies a change in the magnitude of G.
However, a potential of the form
![]() has several
interesting aspects that we will investigate here:
has several
interesting aspects that we will investigate here:
A) Although repelling by nature, it can substantially enhance the gravitational acceleration in the
limit of large distances from the center of the potential, as well as yield standard Newtonian dynamics as r ![]() 0.
0.
B) It suggests a force acting over a 4 dimensional, real spatial manifold.
An obvious characteristic of the superposition of an inverse-cube repelling
force with an inverse-square attracting force is that it establishes and
requires a length scale to be invoked. Only at one particular separation of an
![]() pair will the magnitudes of the field strengths be equal. Thus, if this
separation of an isolated M-
pair will the magnitudes of the field strengths be equal. Thus, if this
separation of an isolated M-![]() pair is given as
pair is given as ![]() , any perturbation of
either particle tends toward equilibrium. (By equilibrium, we mean
here that the absolute value of the two fields are equal). If the separation
is increased, the inverse-square attractive term dominates (thereby decreasing the
separation ), while if the separation is decreased, the
inverse-cube repelling term dominates (thereby sending the system back toward
larger values of the separation).
, any perturbation of
either particle tends toward equilibrium. (By equilibrium, we mean
here that the absolute value of the two fields are equal). If the separation
is increased, the inverse-square attractive term dominates (thereby decreasing the
separation ), while if the separation is decreased, the
inverse-cube repelling term dominates (thereby sending the system back toward
larger values of the separation).
At equilibrium, we have:
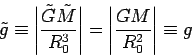 |
(1) |
 |
(2) |
Note that this distance scale is merely a currently observed quantity, and as such, does not in principle depend on the time history of the Universe. If the Universe is flat or open, this scale length can exist at all epochs. Thus, we don't necessarily need to invoke time variability of fundamental constants. If the Universe is closed, there will be an epoch where the scale factor implies global distances smaller than 100 Mpc, but this still does not rule out anything that follows here.
In any event, we bear in mind that this value is just a working hypothesis, and has no real effect on our conclusions for dynamics, since the product of ![]() and
and
![]() is all that appears in every calculation.
However, we shall see in section 3 that our ``guess" is apparently quite close to a value that redefines the Planck scales in a strikingly reasonable way, and also (in section 4) that this provides a natural value of the density of
is all that appears in every calculation.
However, we shall see in section 3 that our ``guess" is apparently quite close to a value that redefines the Planck scales in a strikingly reasonable way, and also (in section 4) that this provides a natural value of the density of
![]() to explain the apparent acceleration of the Hubble flow. In this regard, it is useful to point out, that as a repelling field, it will will be smooth over large distances, being characterized as a fluid with some density
to explain the apparent acceleration of the Hubble flow. In this regard, it is useful to point out, that as a repelling field, it will will be smooth over large distances, being characterized as a fluid with some density ![]() . We consider this idea below.
. We consider this idea below.