Solutions to homework set 1
1.1
There is more than one way to prove this, but I'll choose one of
the more straightforward:
Assume perfectly circular orbits, and that the two planets start at
conjunction.
let A_e be the angular position of the earth,
A be the angular position of the planet.
T_e is the sidereal period of the earth,
T is the sidereal period of the planet
At any time, t, the angular position of the earth as measured from
conjunction is:
A_e(t) = 2*pi*t/T_e. Likewise for the planet:
A(t) = 2*pi*t/T.
i) An inferior planet will completely circle the sun and reach the
next conjunction with earth before the earth has completed one sidereal
period. The planet will have travelled exactly 2*pi further than the earth
has, so that at the next conjunction, t=S, and
A_e(S) = A(S) - 2*pi, so that:
2*pi*S/T_e = 2*pi*S/T - 2*pi. Solving for S gives:
S(1/T - 1/T_e) = 1, so that 1/S = 1/T - 1/T_e.
ii) The earth will completely circle the sun and reach conjunction with a
superior planet before that planet has completed a period. So, analogous to
the above:
A(S) = A_e(S) - 2*pi, so that solving for S gives:
S(1/T_e - 1/T) = 1, and 1/S = 1/T_e - 1/T
1.3
a) Using equation 1.1 and solving for the sidereal periods gives:
S_v = 583.9 day
S_m = 779.9 day
P_e = (sidereal period of earth) = 365.5 day
venus: P_v = (S_v*P_e)/(S_v+P_e) = 224 day
mars : P_m = (S_m*P_e)/(S_m+P_e) = 687 day
b) Mercury has the shortest synodic period because its small sidereal period
enables it to lap the earth quicky. Mercury's sidereal period is 0.2408yr,
so that sometime between 0.2408yr and 0.4816yr, it will again
be in conjunction with the earth. Again using equation 1.1 for Mercury
shows that its synodic period is 0.312 yr.
The second most popular answer was Pluto, but Pluto can't have a smaller
synodic period than Mercury because the earth will take a little more than
one year to lap Pluto. Pluto does have the smallest synodic period
amongst the superior planets, but Mercury has the smallest among all
the planets.
1.4
| For the sun: | RA(hour) | dec (degrees) |
| Vernal equinox: | 0 | 0 |
| Summer solstice: | 6 | 23.5 |
| Autumnal equinox: | 12 | 0 |
| Winter solstice: | 18 | -23.5 |
c.f. Figure 1.11
The declination of 23.5 is the angle between the earth's equator and
the ecliptic.
1.5
The altitude, h, of the sun as it passes meridian at latitude L
is:
h = 90 - (L - dec)
i) summer solstice: The sun's declination, dec, is 23.5 degrees,
so, at latitude 42 degrees,
h = 90 - (42 - 23.5) = 71.5 degrees
ii) winter solstice: The sun's declination, = -23.5 degrees,
so,
h = 90 - (42 + 23.5) = 24.5 degrees
1.6
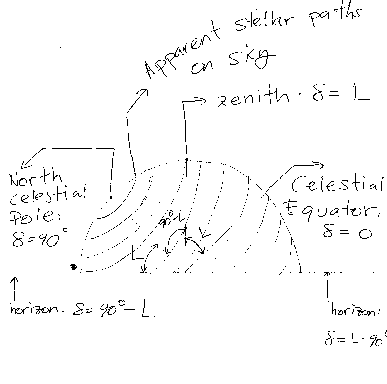
a) As shown in the above figure, at latitude L, the north pole or declination of
90 degrees lies at an altitude of L degrees above the horizon. The
zenith lies where the declination is L, and horizon lies at
declination (90-L) degrees. Always visible circumpolar stars will
never set, and these are the stars whose declinations lie between
90 degrees and (90-L) degrees (if L is greater than 0). If you're in the southern hemisphere,
with L<0, The declination of the (south) celestial pole is -90
degrees, and stars with declinations
between -90 degrees and (-90-L) degrees will always be visible.
b) At summer solstice, the sun lies at declination 23.5 degrees. Using the
result from part a, the sun never sets in those latitudes
where the declination > 90 -L, or,
23.5 degrees > 90 -L, so that
L > 90 - 23.5 = 66.5 degrees, i.e. for latitudes within the arctic circle.
c) at vernal equinox, the sun lies essentially at declination 0 degrees.
Now, the equinox means that every point on earth will experience equal
amounts of darkness and sunlight that day. So, that implies that there
is no place on earth where the sun never sets. Strictly speaking, it
can be argued that the poles ARE the only place where the sun never sets,
because there, the sun just orbits the horizon. So, the sun never rises
and consequently never sets.
You can also use part a) to argue that no latitude can be found
which satisfies 0 > 90 -L.
