 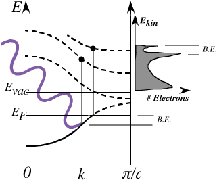 

(a) Cuprate superconductor levitates a magnet, (b) Band structure and
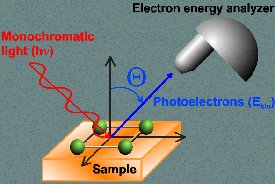
density of states of a material probed by ARPES (c) ARPES (Angle resolved
photoemission spectroscopy) technique (d) Richard P. Feynman
Many body physics provides the framework for understanding the collective
behavior of interacting electrons in a material. This course provides an
introduction to the field, familiarize you with the main techniques and
concepts, aiming to give you first-hand experience in calculations and problem
solving using many body methods.
Class Time: ARC building (204), 12:10pm-1:30pm every Monday and Thursday
| Instructor: |
Kristjan Haule
Office: Serin E267
email: haule@physics.rutgers.edu
Phone: 445-3881
Office hours: Friday 4:45pm
|
Literature: The course will be built from the three excellent books:
- Condensed Matter Field Theory by Alexander Atland and Ben Simons
Most of the course is build from this bool. It is a modern textbook on Field Theory with strong emphasis
on modern tools like Functional field integral.
- Quantum Many-particle Systems by J.W. Negele, H. Orland
Excellent coverage of perturbation theory using Functional field integral language. We will use it in the chapter on perturbation theory.
- Many-Particle Physics by Gerald D. Mahan
A classical textbook dealing in detail with response functions such as Green's function and optical conductivity, Kubo formalism and many more.
We will add a small bits and pieces from this book, mostly in the chapter on the perturbation theory & uniform electron gas.
Other good references:
- Introduction to Many Body Physics by Piers Coleman
Very exhaustive reference with particular emphasis on correlations.
- Methods of Quantum Field Theory in Statistical Physics by A.A. Abrikosov, L.P. Gorkov, I.E. Dzyaloshinski
Classic text from the sixties, known usually as AGD. Technically a
bit more involved but contains many derivations which can not be found in any other book.
- Basic Notion of Condensed Matter Physics by P.W. Anderson
Great inspiration from one of the "fathers" of strongly correlated field
- Quantum Theory of Many-Particle Systems by A.L. Fetter and J.D. Walecka
- Field Theories of Condensed Matter Systems by Edwardo Fradkin
Interesting material on the fractional statistics and the fractional quantum Hall effect.
- Introduction ot Superconductivity by Michael Tinkham
Great book on supeconductivity.
- Interacting Electrons and Quantum Magnetism by Assa Auerbach
- Quantum Field Theory in Condensed Matter Physics by Alexei M. Tsvelik
Very good for one dimensional systems.
Lecture Notes from 2022 in pdf
Homeworks from 2022
Homework 1
Homework 2
Homework 3
Homework 4
Course Outline and List of Topics
- Quantum fields
- Second quantization
- Applications of second quantization:
- Jellium model
- Tight binding model
- Mott Hubbard transition and Spin models of Mott insulator
- Interacting fermions in 1D
- Quantum spin chain
- Feynman path integral
- Functional field integral
- Green's function at zero temperature and finite temperature (Matsubara formalism)
- Perturbation Theory
- Plasma theory of interacting electron gass
- Bose-Einstein condensation and superfluidity
- Superconductivity & BCS Theory
Students with Disabilities
|



