Rutgers Physics 385 Electromagnetism I (Fall15/Gershtein)
Homework 12 - Due TUESDAY December 8, 2015 in class
1) Verify that for uniform magnetic field the potential is
.
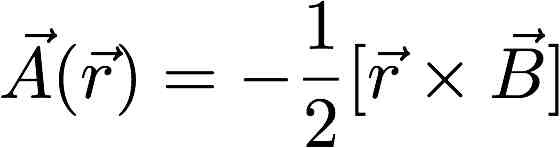That is, check that divergence of the potential is zero and curl is B.
2) A uniform surface current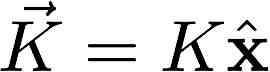 
flows along the xy plane. Find the magnetic potential.
3) Show that the magnetic field of a dipole can be written in coordinate-free form:
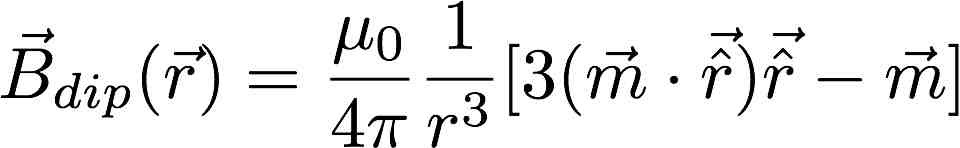
4) Find the exact magnetic field a distance z above the center of a square loop of side w carrying current I.
Verify that it reduces to a dipole field for z>>w, with the appropriate dipole moment (what is it?).
5) An infinitely long cyllinder carries a uniform magnetization M parallel to its axis. Find the magnetic field due to M
inside and outside the cyllinder.
6) An iron rod of length L and square cross section (side a) is given a uniform longitudinal magnetization M, and then bent into a a circle
with a narrow gap between (width w). Find the magnetic filed at the center of the gap. Assume thar w << a.
Hint: note the similarity between this problem and problem 4) from HW02 .
7) A coaxial cable consists of two very long cylindrical tubes (radii a and b),
separated by linear material of magnetic susceptability χm. A current I
flows down the inner conductor and returns along the outer one; in each case the current uniformly distributes itself over the surface of the tubes.
a) Find the magnetic field in the region between the tubes
b) As a check, calculate the bound currents, and confirm that they, together with the free currents, generate correct field.