Rutgers Physics 385 Electromagnetism I (Fall15/Gershtein)
Homework 10 - Due November 19, 2015 in class
1) The space between the plates of a parallel-plate capacitor is fille with dielectric material whose
dielectric constant εr varies linearly from 1 at the bottom plate
(x=0)
to 2 at the top plate
(x=d). The capacitor is connected to a batterry of voltage
V.
Find all bound charge and check that it is zero.
2) At the interface between one linear dielectric and another, the electric field lines bend:
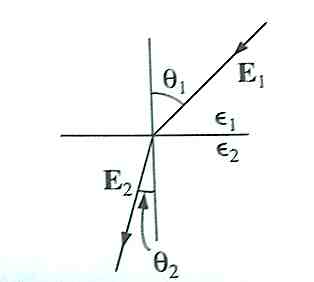
Show that
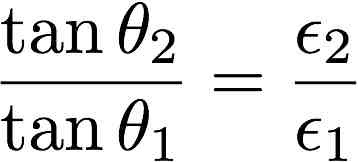
assuming that there is no free charges at the boundary.
3) A particle of charge q enters a region of uniform magnetic field B
(pointing into the page):
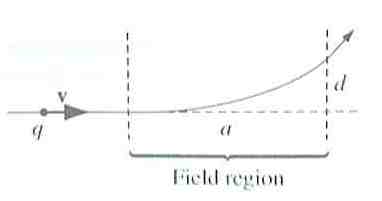
Is the charge of the particle positive or negative?
Find the momentum of the particle in terms of q, a, d, and B.
4) For Example 5.2 in the book - the one we did in class - about crossed electric and magnetic fields,
E pointing along z and B pointing along x, find and sketch the trajetcory of the particle for initial
conditions where it starts at the origin, but with a non-zero velocity:
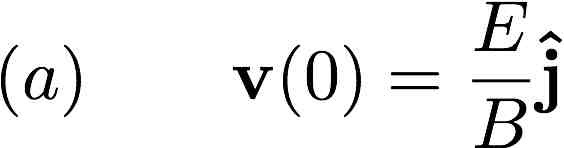
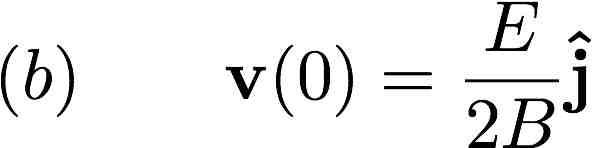
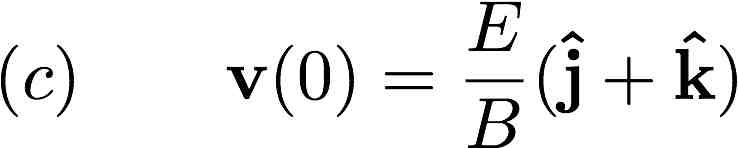
5) In 1897, J.J. Thompson discovered electron by measuring the charge-to-mass ratio of "cathode rays" (actually,
streams of electrons knocked out of the cathode) as follows:
a) First he passed the beam through uniformed crossed electric and magnetic fields (mutually perpendicular, and each perpendicular to the beam)
and adjusted electric field until he got no deflection (i.e. electric force compensated the magnetic). In terms of E and B, what was the
speed of the particles?
b) Then, he turned off the electric field and measured the radius of curvature of the beam, R, as deflected by the magnetic field alone.
In terms of E, B, and R, what is the charge-to-mass (q/m) ratio of the particles?

