Rutgers Physics 385 Electromagnetism I (Fall15/Gershtein)
Homework 2 - Due September 17, 2015 in class
1) Suppose the electric field in some region is found to be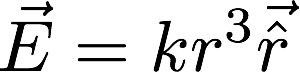 
,
in spherical coordinates (k is some constant).
(a) Find the charge density ρ
(b) Find the total charge contained in a sphere of radius R centered at the origin (there are many ways to do it, pick at least two, and do it both ways)
(c) Calculate the divergence of the field in both spherical and
cartesian coordinates. See the inside front of Griffiths for any formulae.
2) A charge q sits at the back corner of a cube as shown in the figure below
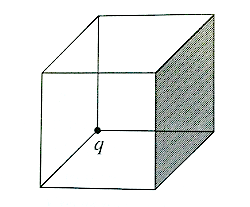
What is the flux of the electric field trough the shaded side?
Note: This is a simple problem and no algebra is necessary. Use symmetry
and just count the number of faces.
3) A solid sphere of radius R is charged with the uniform charge density ρ.
Find the electric field as a function of distance from the center of the sphere.
4) The sphere from the previous problem is placed so its center is at (0,0,0).
A spherical hollow cavity is made inside it. The
center of the hollow has coordinates (0,0, R/2), and the radius of the hollow is R/4.
(a) calculate the electric field for points along the Z axis i.e. (0,0,z)
(b) calculate the electric field for points along the X axis i.e. (x,0,0)
Hint: use superposition principle, and remember that you can always view empty space as
space filled with both positive and negative charges with the same density.