Instructor:

       Piers Coleman 
       Room 268 Serin 
       Tel. 445-5082 
       email:  coleman@physics.rutgers.edu

Scope of Course. This course is aimed to provide an advanced foundation for any research involving quantum mechanics. The course follows develops Dirac's bra-ket approach, developing the formalism and providing worked examples of some of the most recent lines of thought and applications of quantum mechanics such as quantum computation, Berry's geometric phase, 2D electron gasses and Quantum Entanglement. Texts:

       J. J. Sakurai      Modern Quantum Mechanics     (Addison Wesley, 1994)
       R. Shankar         Principles of Quantum Mechanics 
       G. Baym            Lectures on Quantum Mechanics (Addison Wesley, 1990)
       P.A.M. Dirac       Quantum Mechanics (Cambridge)

Assessment: Assessment will be made on the basis of weekly assignments  (502), a mid-term and final exam.
(Old assignments for 501).

Tentative Outline for the Course

Fall:

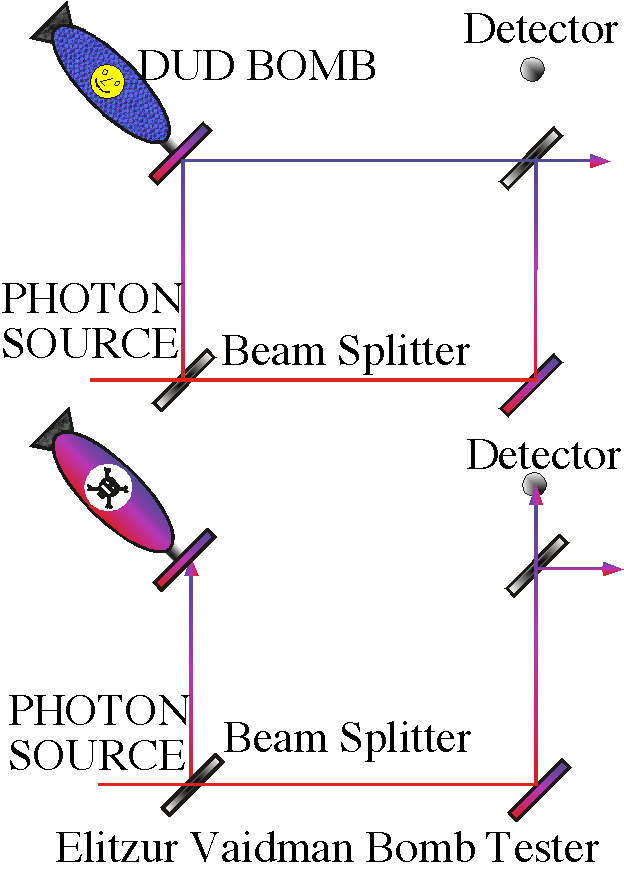
• Fundamental Concepts. Historical Background ; Photon polarization and the Stern-Gerlach experiment; bra-ket formalism; the Copenhagen interpretation- modern view of measurement theory- Elitzur-Vaidman bomb problem; Uncertainty Principle; momentum and position representations.
• Quantum Dynamics Hamiltonian as the generator of time-translation; Schrödinger/Heisenberg ; Simple-harmonic oscillator; Schrödinger's wave equation; Hydrogen atom and the Quantum Stadium; Propagators and Path Integrals; Aharanov Bohm effect; Electron in a magnetic field and the fractional quantum Hall Effect.
• Angular Momentum Rotation group; SU(2) and SO(3); density matrices; Addition of angular momentum; Berry Phases; EPR Paradox and Bells inequality;  Quantum Teleportation. Vector and Tensor operators; Wigner Eckert Theorem and applications.

• Symmetries.  Quantum vs classical symmetries. Discrete Symmetries.   Parity. Transformation of operators and states.  Lattice translation:  conservation of crystal momentum and Bloch's theorem. Time-reversal symmetry.  Anti-unitary operators.   Transformation of position, momentum and orbital angular momentum. Transformation of spins under time-reversal.   Kramers theorem.
• Approximate methods: Perturbation Theory and Variational approach. Time independent perturbation theory: 1st and 2nd order. Wavefunction renormalization. Degenerate perturbation theory.  Fine structure in  Hydrogen-like  atoms.  Zeeman effect. Van der Waals forces.  Variational methods. Time dependent potentials and the "interaction representation". Spin resonance and the Maser. Time dependent perturbation theory: transition rate and Golden Rule. Absorption and emission of radiation: dipole approximation. Photo-electric effect.  Line broadening and resonances.
• Identical Particles .  Exchange symmetry. Symmetrization postulate. Pauli Exclusion principle. Two electron system. Helium atom. Occupation number representation. Creation and annihilation operators.  Fermions and Bosons.  Hamiltonian of many particles.
• Scattering Theory. Separation of wave into incoming and scattered components. Lippmann Schwinger equation.  Scattering amplitude and phase shift. Scattering cross-section.  Born approximation.  Coulomb scattering. Beyond Born approximation. Optical Theorem.  Phase shift at high energy- eikonal approximation.  Partial wave decomposition.  Calculation of phase shift. Hard sphere scattering.  Low energy scattering and bound states. Resonant scattering.  Scattering of identical particles.  Symmetry in scattering.  Time dependence in scattering.  Inelastic scattering.
• Relativistic Quantum Mechanics.  Klein Gordon model and its failure.   Dirac equation.  Concept of antiparticle.  Emergence of spin.